1.数据结构与算法
1.1 数据结构的定义
1 | 数据结构=数据+算法 |
1.1.1 数据与信息
数据:指的是一种未处理的原始文字,数字,符号、图形
信息:当数据 –处理【算法+数据结构】–> (特定的方式系统地处理、归纳甚至进行分析)
1.1.2 数据的分类
- 1.按照计算机中所存储和使用的对象:
1.1 数值数据: 如0,1,2…,9所组成,可用运算符来进行运算的数据
1.2 字符数据: 如A,B,C,…,+,*等非数值型数据
- 2.按照数据在计算机程序设计语言中的存在层次:
2.1 **基本数据类型/标量数据类型**: 不能以其他类型来定义的数据类型。【Java中所有基本数据类型】
2.2 **结构数据类型/虚拟数据类型**: 【字符串,数组,指针,列表,文件等】
2.3 **抽象数据类型**: 可以将一种数据类型看成是一种值的集合,以及在这些值上所进行的运算和其所代表的属性所成的集合【堆栈等】1.2 算法
1 | 可执行程序=数据结构+算法【最关键的因素】 |
1.2.1 算法的定义
1 | 为了解决某项工作/某个问题,所需要有限数量的机械性/重复性指令与计算步骤 |
算法的五个条件:
算法的特性 内容与说明 输入 0-n个输入,这些输入必须有清楚的描述或定义 输出 1-n个输出【至少有一个输出结果】 明确性 每个指令/步骤必须是简洁明确的 有限性 在有限步骤后一定会结束【不存在无限循环】 有效性 步骤清楚+可行【能让用户】 算法的分类:
描述工具 具体描述 举例 伪语言 不能直接放入计算机执行的语言,一般需要一种特定的预处理器/人工编写转换成真正的计算机语言 sparks,pascal-like 表格/图形 清晰明了的描述过程 数组,树形图,矩阵图 流程图 图形符号表示法 流程图 程序设计语言 可读性高的高级语言 Java,python,c#
1.3 算法性能分析
1.3.1 时间复杂度
1 | 1.一种以概量方式来衡量运行时间 |
1.3.2 空间复杂度
1 | 1.一种以概量方式来衡量所需的内存空间 |
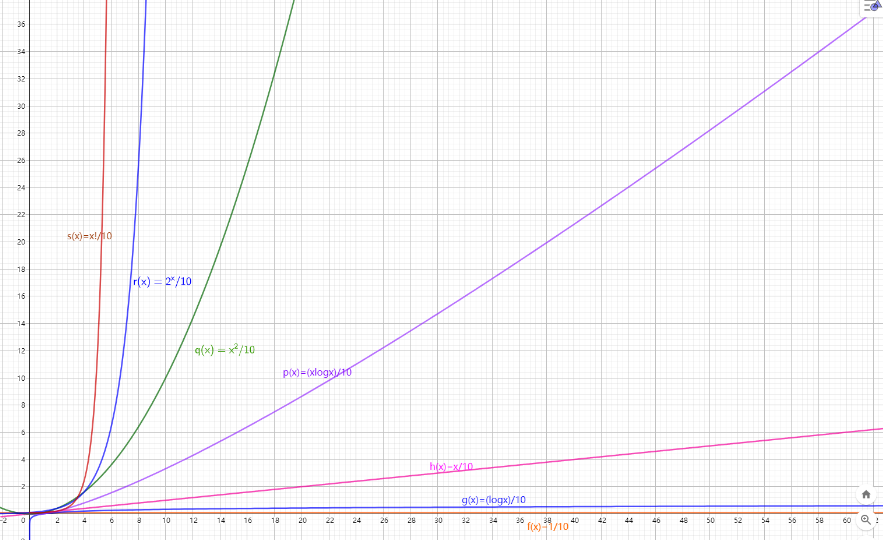
1.3.3 Big-oh(衡量时间复杂度)
1 | 常见的算法时间复杂度: |
1.4 常见算法
1.4.1 分治法
1.4.2 递归法
1.4.3 贪心法
1.4.4 动态规划法
1.4.5 迭代法
1.4.6 枚举法
1.5程序设计简介
1.5.1 程序开发流程
四项原则
1
2
3
41.可读性高:阅读和理解都相当容易
2.平均成本低:成本考虑不局限于编码的成本,还包括执行,编译,维护,学习,调试和日后更新等成本
3.可靠性高:所编写出来的程序代码稳定性高,不容易出现边际错误
4.可编写性高:对于针对需求所编写的程序相对于容易
2.数组结构
2.1 线性表
- 线性表的定义:
有序表可以是空集合/(a1,a2,a3,….an-1,an),存在唯一的第一个元素a1和存在唯一的最后一个元素an。除了最后一个元素都有后继者,除了第一个元素都有先行者。
- 线性表的运算:
1.计算线性表的长度n
2.取出线性表中的第i项元素来修改 3.插入一个新元素到第i项,并将原来位置和后面元素都后移
4.删除第i项元素
5.遍历读取线性表元素
6.替换第i项元素 7.复制线性表
8.合并线性表
- 线性表的存储方式:
| 静态数据结构 | 动态数据结构 | |
|---|---|---|
| 形式 | 密集表 | 链表 |
| 优点 | 使用连续分配的内存空间来存储有序表元素 设计简单,读取和修改表中任意元素时间固定O(1) |
使用不连续的内存空间来存储 数据插入和删除都方便O(1) O(n)内存分配是在程序执行时才分配,不需要事先声明,充分节省内存 |
| 缺点 | 删除和加入数据,需要挪动大量数据O(n) | 不能随机读取,必须按顺序遍历找到数据O(n) |
2.2 数组
2.2.1 一维数组

2.2.2 二维数组

2.3 矩阵
3.链表
- 许多相同数据类型的数据项,按照特定顺序排列而成的线性表(2.1定义的)
3.1 动态分配内存
| 对比项目 | 动态配置 | 静态分配 |
|---|---|---|
| 内存分配 | 运行阶段 | 编译阶段 |
| 内存释放 | 程序结束前必须释放分配的内存空间,否则会内存”泄露” | 不需要释放,程序结束时自动归还给系统 |
| 程序运行性能 | 比较低(因为所需内存要执行程序时候才分配) | 比较高(程序编译阶段就分配好需要的内存容量) |
| 指针遗失 | 可能会存在内存泄露(程序结束前不释放内存就指向新的内存空间,则原本指向的内存空间就无法被释放) | 没有此问题 |
3.2 单向链表
3.2.1 单链表定义
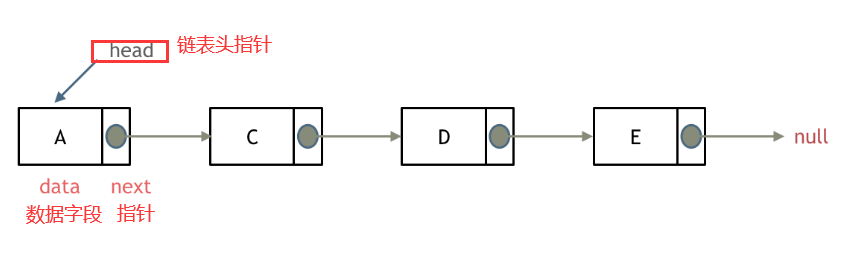
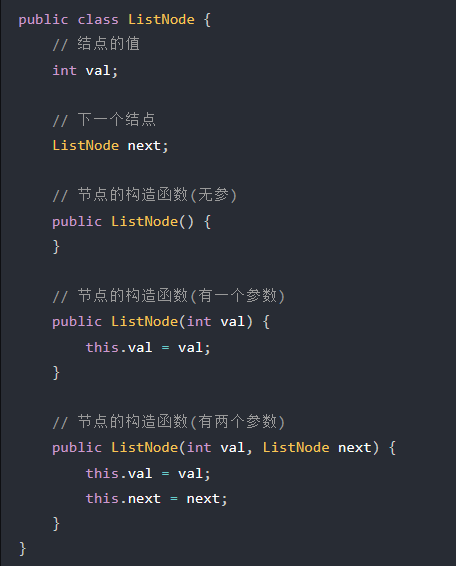
3.2.2 建立单链表
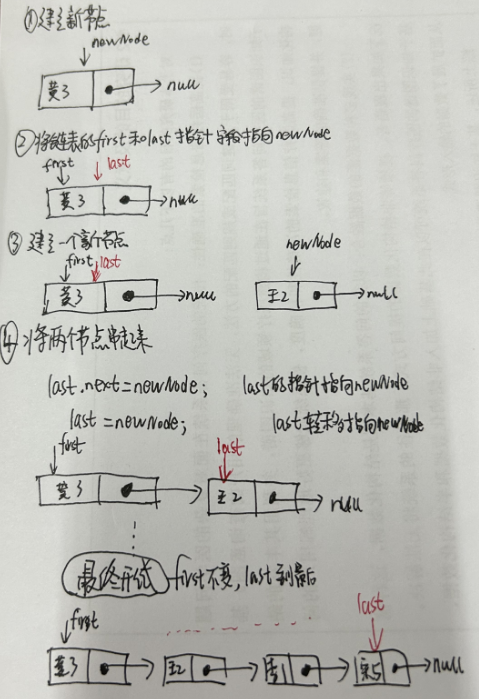
3.2.3 单链表删除节点
- 1.删除链表的第一个节点
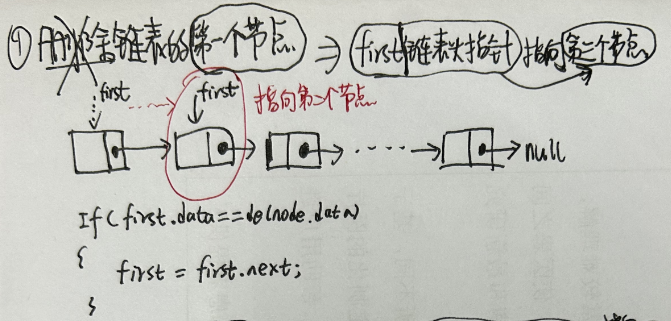
- 2.删除链表的中间节点
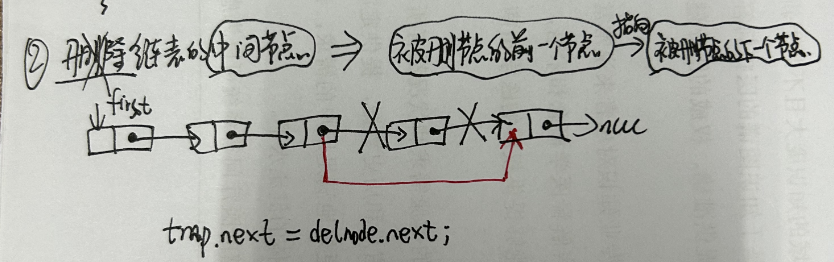
- 3.删除链表的最后一个节点
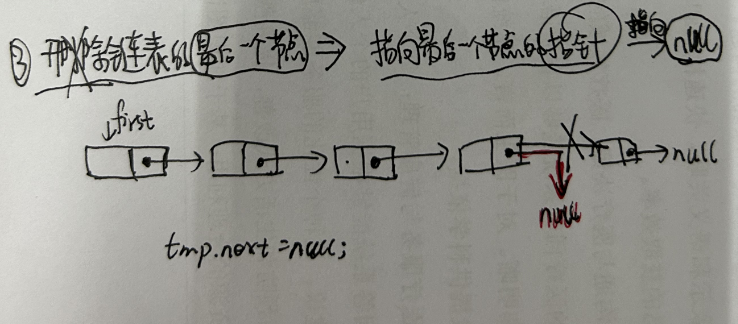
3.2.4 单链表插入节点
- 1.插入到第一个节点前面
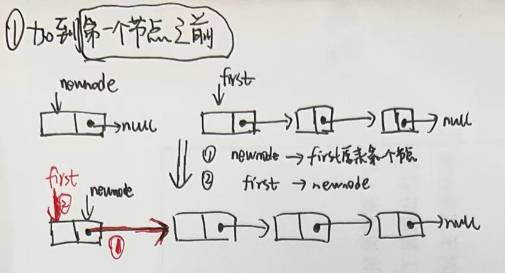
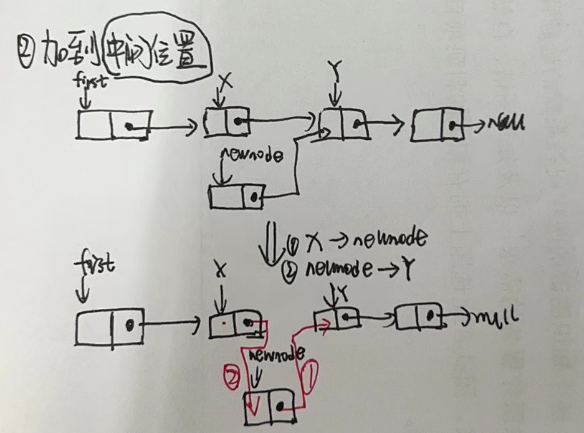
- 2.插入到中间位置
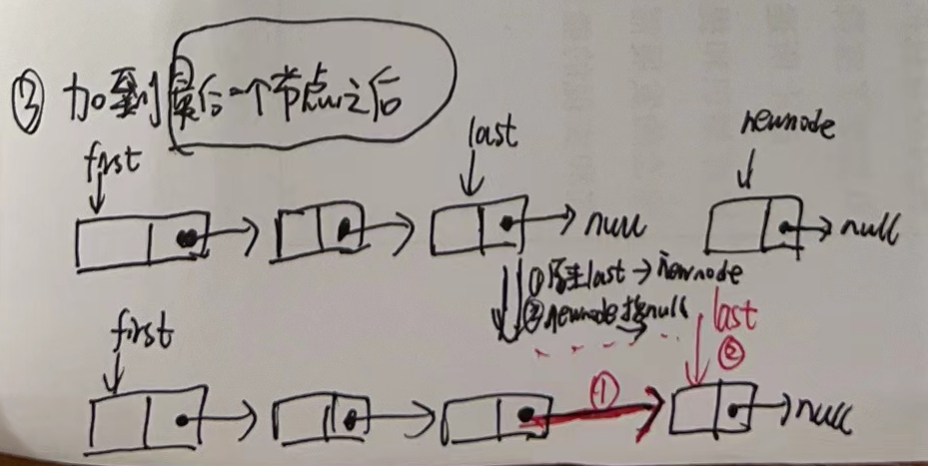
- 3.插入到最后一个节点后面
3.2.5 单链表反转
3.3 环形链表
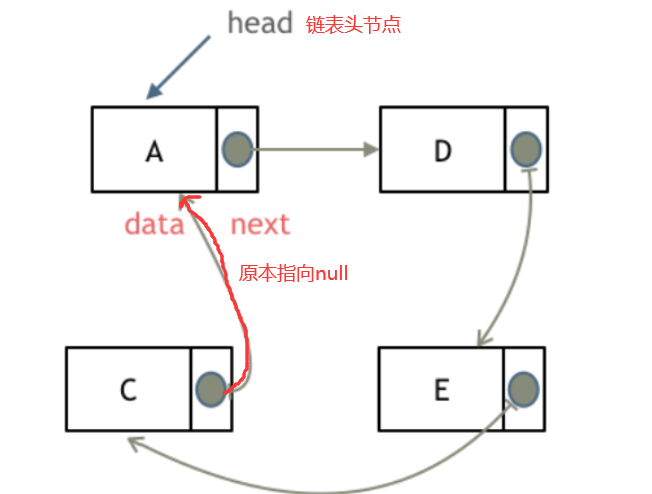
3.3.1 环形链表定义
3.3.2 环形链表插入新节点
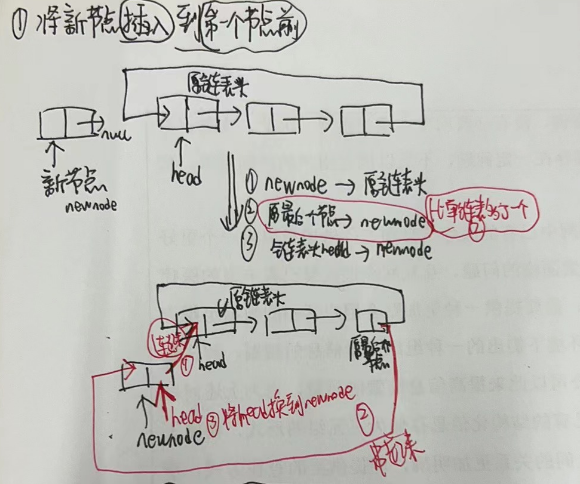
1.插入到第一节点前,成为新的链接头部
2.插入到中间节点部分
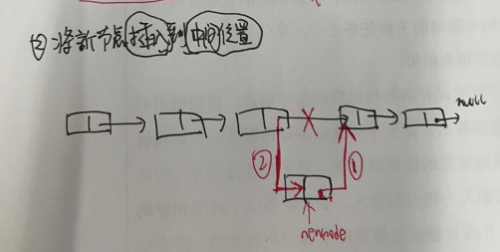
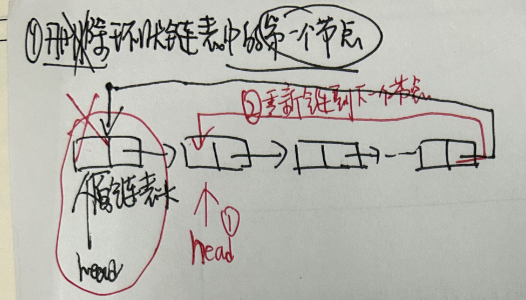
3.3.3 环形链表删除节点
- 1.删除第一个节点
- 2.删除中间节点部分
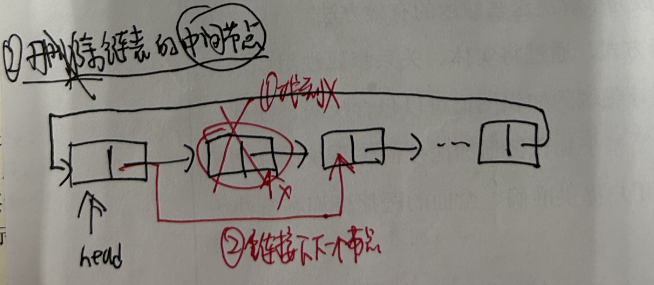
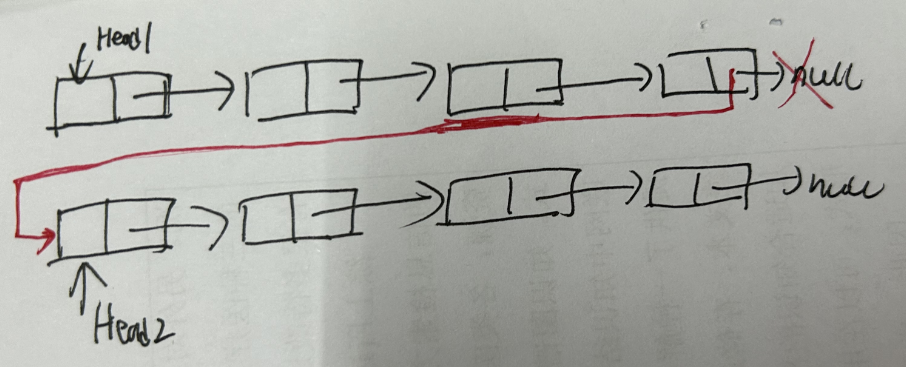
3.3.4 环形链表串联
3.4 双向链表
3.4.1 双向链表定义
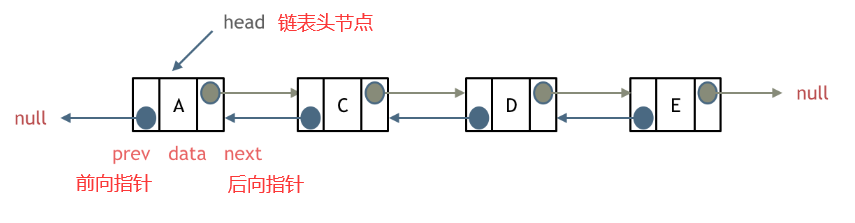
3.4.2 双向链表插入节点
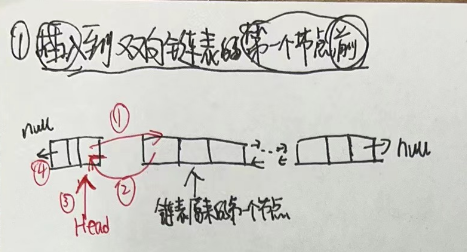
- 1.插入到双向链表的第一个节点前
- 2.插入到双向链表的末尾

- 3.插入到双向链表的中间位置
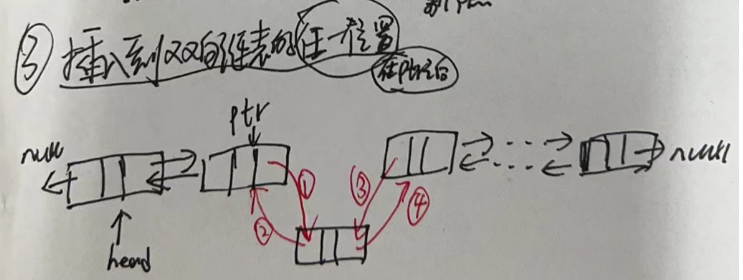
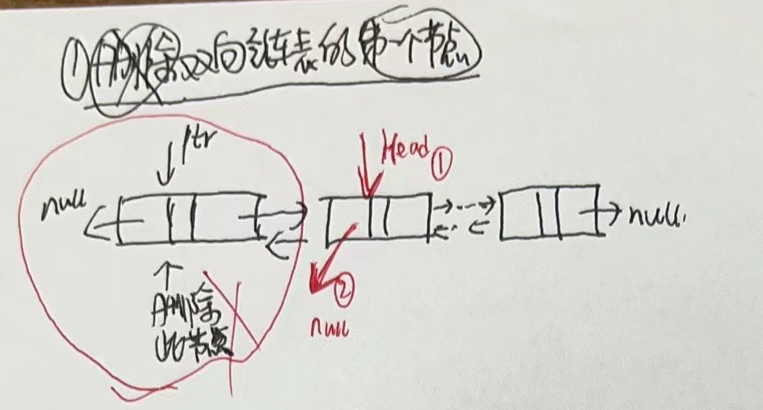
3.4.3 双向链表删除节点
- 1.删除双向链表的第一个节点
- 2.删除双向链表的最后一个节点

- 3.删除双向链表的中间位置



