预备知识
数据操作

数据操作实现
读取和存储数据
1
2
3
4
5
6
7
8
9
10
11
12
13
| import torch
#随意0-12
x=torch.arange(12) #使用arange创建一个行向量x
print(x)
print(x.shape) #根据张量的shape属性来访问张量的形状
print(x.numel()) #获取张量中元素的总数(形状的所有元素乘积,检查它的大小)
print(x.reshape(3,4)) #改变张量的形状 但是不改变元素数量和元素值 # x.reshape(-1,4) / x.reshape(3,-1) 通过-1来调用此自动计算出维度的功能
#全0
print(torch.zeros(2,3,4))
#全1
print(torch.ones(2,3,4))
#正态分布(均值0,标准差1)
print(torch.randn(3,4))
|

运算符
1
2
3
4
5
6
7
8
9
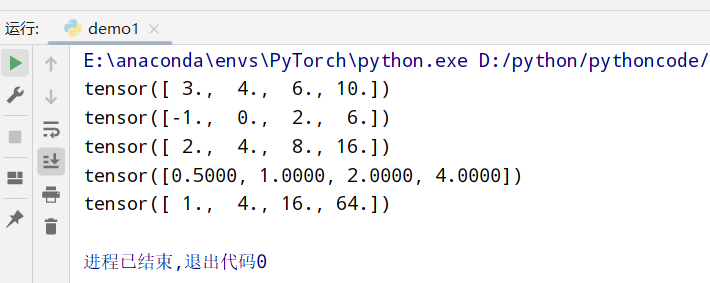
| import torch
#进行四则运算
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
print(x+y)
print(x-y)
print(x*y)
print(x/y)
print(x**y)
|
广播机制
1
2
3
4
5
6
7
8
9
10
11
12
| #1.通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状。
#2.对生成的数组执行按元素操作。
import torch
a = torch.arange(3).reshape((3, 1)) # 3*1矩阵
b = torch.arange(2).reshape((1, 2)) # 1*2矩阵
print(a)
print(b)
#如果a+b的话因为两个形状不匹配 --> 广播成更大的3*2矩阵
#a将复制列
#b将赋值行
print(a+b)
|

索引和切片
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
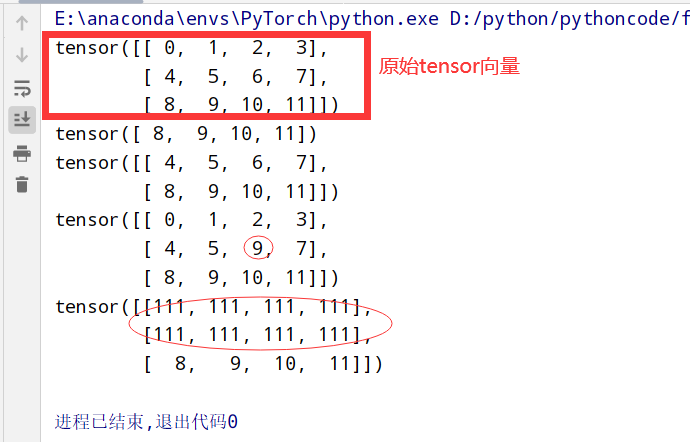
| import torch
x=torch.arange(12).reshape((3, 4))
print(x)
#输出最后一个元素
print(x[-1])
#输出第二个和第三个元素
print(x[1:3]) #下标第一行和第二行
#指定索引写入一个
x[1,2]=9 #第二行第三个元素改为9
print(x)
#指定索引写入很多
x[0:2,:]=111 #第一行和第二行的所有列都改为111
print(x)
|
节省内存(创建一样大的0矩阵)
1
2
3
4
5
6
7
8
9
10
11
12
13
| import torch
#原来的问题!!
Y=torch.arange(12).reshape((3,4))
X=torch.arange(12).reshape((3,4))
before=id(Y)
Y=Y+X
print(id(Y)==before) #Y被赋值新的内存,执行内存中新位置
#原地更新
Z=torch.zeros_like(Y) #创建一个和Y一样大的
print(id(Z))
Z[:]=X+Y
print(id(Z))
|

深度学习框架定义的张量->Numpy张量(ndarray)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| import torch
import numpy as np
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
A=X.numpy()
B=torch.tensor(A)
print(type(A)) #ndarray数组
print(type(B)) #tensor向量
#调用item函数/Python内置函数
a=torch.tensor([3.5])
print(a)
print(a.item()) #调用item函数!!转变为ndarray数组
print(float(a))
print(int(a))
|

数据预处理(Pandas)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
import torch
import numpy as np
import pandas as pd
import os
#1.读取数据集
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv') #创建 ../data/house_tiny.csv文件
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n') # 列名
f.write('NA,Pave,127500\n') # 每行表示一个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
data=pd.read_csv(data_file)
print(data)
print()
#2.处理缺失值(插值法和删除法)
inputs=data.iloc[:,0:2] #利用位置索引iloc --> data前两列为inputs data最后一列为outputs
outputs=data.iloc[:,2]
inputs=inputs.fillna(inputs.mean()) #利用均值填充
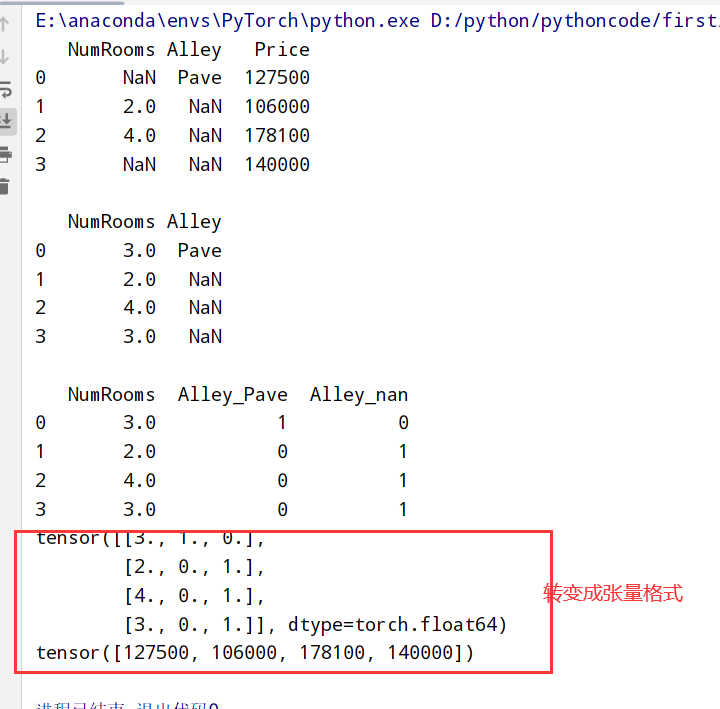
print(inputs)
print()
##对于inputs中的类别值/离散值
##Alley里面有Pava和NaN两种类型 --> pandas可以自动将此列分为两列(Alley_Pave[设置1]和Alley_nan[设置0]) 缺少的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1
inputs=pd.get_dummies(inputs,dummy_na=True)
print(inputs)
#3.转换为张量格式(数值类型-->张量类型) torch.tensor()函数
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
print(X)
print(y)
|
线性代数
标量/向量/矩阵/张量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
import torch
import numpy as np
import pandas as pd
import os
#1.标量
x=torch.tensor(3.0)
y=torch.tensor(2.0)
print("x+y:",x+y)
print("x-y:",x-y)
print("x*y:",x*y)
print("x/y:",x/y)
print("x**y:",x**y)
print()
#2.向量([标量值1,标量值2,...,标量值N]) 一阶张量
x=torch.arange(4)
print("x:",x)
print()
#3.矩阵([向量1,向量2]) 二阶张量
A=torch.arange(20).reshape(5,4) #5行4列
print("A:",A) #输出A矩阵
print("A的转置:",A.T) #输出转置
##两个形状相同的矩阵相加
A=torch.arange(20, dtype=torch.float32).reshape(5, 4)
B=A.clone()
print("A:",A)
print("A+B:",A+B)
print()
#4.张量(大写字母)
##处理图像 -->n维数组[高度轴(Red红色)/宽度轴(Green绿色)/通道轴(Blue蓝色)]
X=torch.arange(24).reshape(2,3,4)
print("X:",X)
print()
|

降维
降维求和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
import torch
import numpy as np
import pandas as pd
import os
x=torch.arange(4,dtype=torch.float32) # 0 1 2 3
print("x:",x)
print("x的总和:",x.sum())
print()
A=torch.arange(20, dtype=torch.float32).reshape(5, 4)
print("A:",A)
print("A的形状:",A.shape)
print("A的总和:",A.sum())
print()
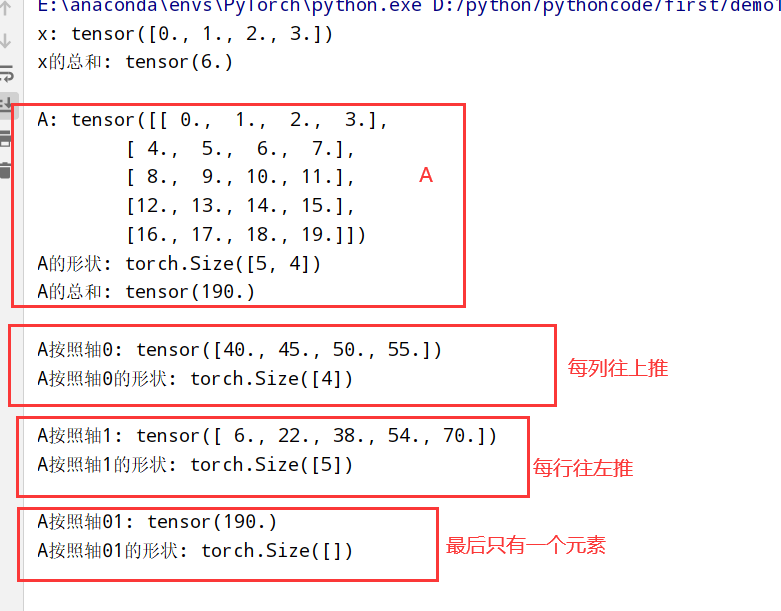
#降维
##每列相加(↑)
A_sum_axis0=A.sum(axis=0) #按照轴0(第一行)将每列往上加到第一个位置[x1,x2,x3,x4]
print("A按照轴0:",A_sum_axis0)
print("A按照轴0的形状:",A_sum_axis0.shape)
print()
##每行相加(←)
A_sum_axis1=A.sum(axis=1) #按照轴1(第一列)将每行往左加到第一个位置[x1,x2,x3,x4]
print("A按照轴1:",A_sum_axis1)
print("A按照轴1的形状:",A_sum_axis1.shape)
print()
##行和列求和
A_sum_axis01=A.sum(axis=[0,1]) #按照轴1(第一列)将每行往左加到第一个位置[x1,x2,x3,x4]
print("A按照轴01:",A_sum_axis01)
print("A按照轴01的形状:",A_sum_axis01.shape)
print()
|
非降维求和(设置keepdims=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
import torch
import numpy as np
import pandas as pd
import os
A=torch.arange(20, dtype=torch.float32).reshape(5, 4)
print("A:",A)
print("A的形状:",A.shape)
print("A的总和:",A.sum())
print()
#非降维求和
sum_A=A.sum(axis=1,keepdims=True) #每行计算往最左边推(行有几个就有几个元素)
print(sum_A)
#沿着某个轴计算A元素的累计总和 --cumsum函数
print(A.cumsum(axis=0)) #第一行=第一行 第二行=第二行+第一行 第三行=第一行+第二行+第三行 ...
|

点积(dot)
1
2
3
4
5
6
7
8
9
10
11
|
import torch
import numpy as np
import pandas as pd
import os
x=torch.arange(4,dtype=torch.float32)
y=torch.ones(4,dtype=torch.float32)
print("x:",x)
print("x:",y)
print(torch.dot(x,y)) # 0*0+1*1+2*1+3*1=6
|

矩阵-向量积(mv)
1
2
3
4
5
6
7
8
9
10
11
|
import torch
import numpy as np
import pandas as pd
import os
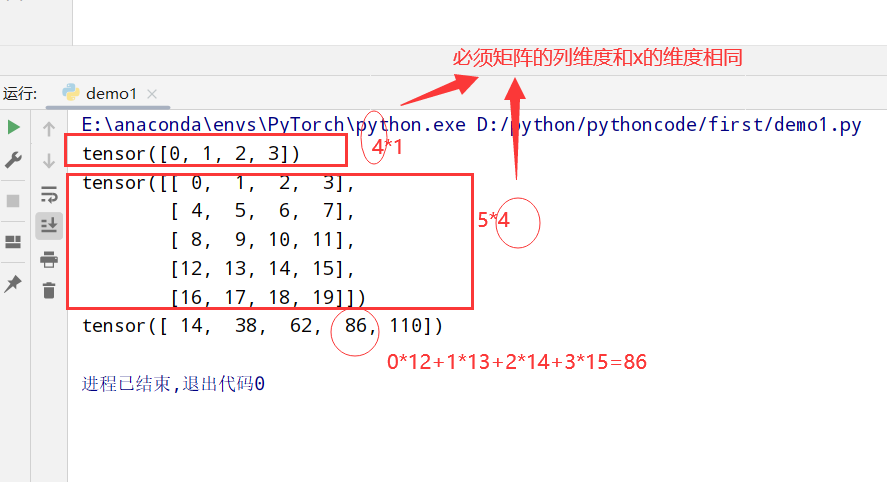
x=torch.arange(4)
A=torch.arange(20).reshape(5,4)
print(x)
print(A)
print(torch.mv(A,x))
|
矩阵-矩阵乘法(mm)
1
2
3
4
5
6
7
8
9
10
11
|
import torch
import numpy as np
import pandas as pd
import os
A=torch.arange(20).reshape(5,4)
B=torch.arange(20).reshape(4,5)
print(A)
print(B)
print(torch.mm(A,B))
|

范数
1
2
3
4
5
6
7
8
9
10
11
12
13
|
import torch
import numpy as np
import pandas as pd
import os
# L2范数(欧几里得距离)
u=torch.tensor([3.0,-4.0])
print(torch.norm(u))
# L1范数(向量元素的绝对值之和)
print(torch.abs(u).sum()) # 3.0+4.0=7.0
print(torch.norm(torch.ones(4,9)))
|

微积分
导数

















