深度学习入门路线
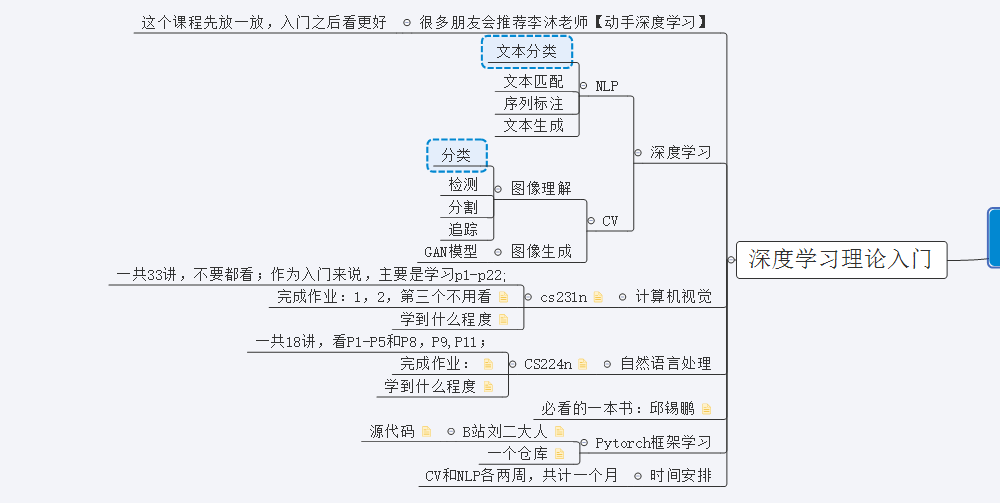
深度学习实战路线
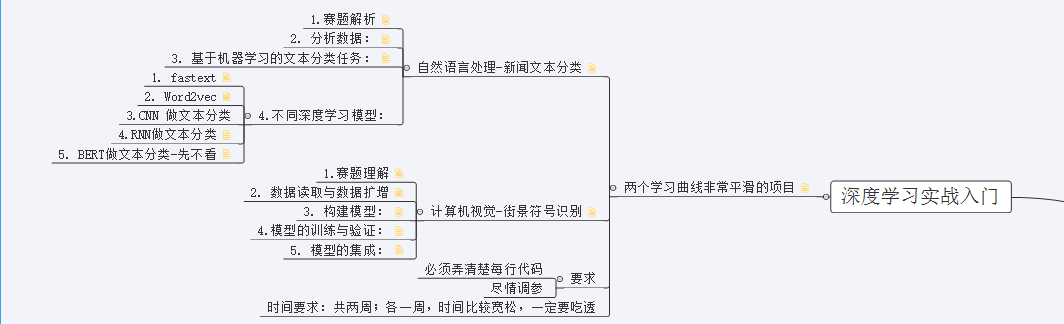
深度学习必看书籍
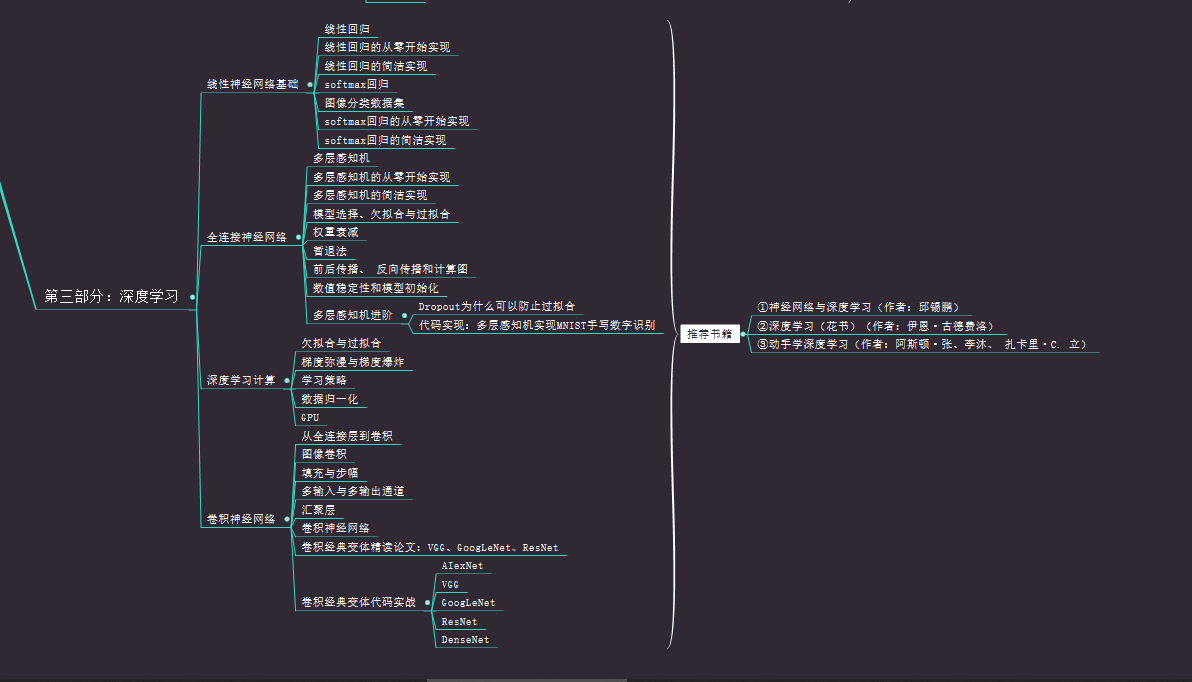
前馈神经网络
总体框架

神经元
人工神经元:
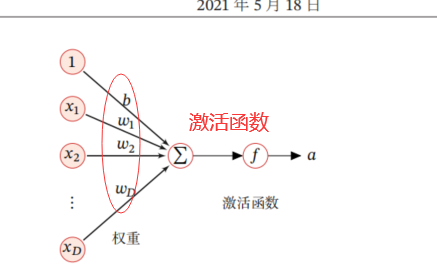
激活函数性质
1
2
3
| 1.连续并可导的非线性函数
2.激活函数及其导数要尽可能简单,有利于提高网络计算效率
3.激活函数的导函数的值域要在一个合适的空间(不能太大也不能太小,否则会影响训练的效率和稳定性)
|
Sigmoid函数(S型曲线函数)
sigmoid函数的公式

1
2
3
4
5
6
| 1.分为logistic函数和Tanh函数
1.1 logistic函数(值域>0):
1.2 Tanh函数(值域(-1,1)):
2.sigmoid函数的性质:
2.1 sigmoid函数是饱和函数[x>-∞和x->+∞时,其f'(x)->0]
2.2 Tanh函数是零中心化的,logistic函数输出恒大于0的
|
sigmoid两种函数的图像:

ReLU函数(斜坡函数/修正线性单元)
ReLU函数公式

1
2
3
4
5
6
7
| 1.优点:
1.1 计算更加高效(采用ReLU的神经元只需要进行加、乘、比较操作)
1.2 具有生物学合理性(单侧抑制、宽兴奋边界) -- 能够保证大约50%的神经元会处于激活状态
1.3 ReLU函数为左饱和函数+x>0时f'(x)=1,在一定程度上缓解了神经网络的梯度消失问题,加速梯度下降的收敛速度
2.缺点:
2.1 输出是非零中心化的,给后一层的神经网络引入偏置偏移,会影响梯度下降的速度
2.2 死亡ReLU问题:ReLU神经元在训练时比较容易"死亡"(如果有一次不恰当的更新后,第一个隐藏层中的某个ReLU神经元在所有训练数据上都不能被激活,在以后的训练过程中永远不能被激活)
|
带泄露的ReLU
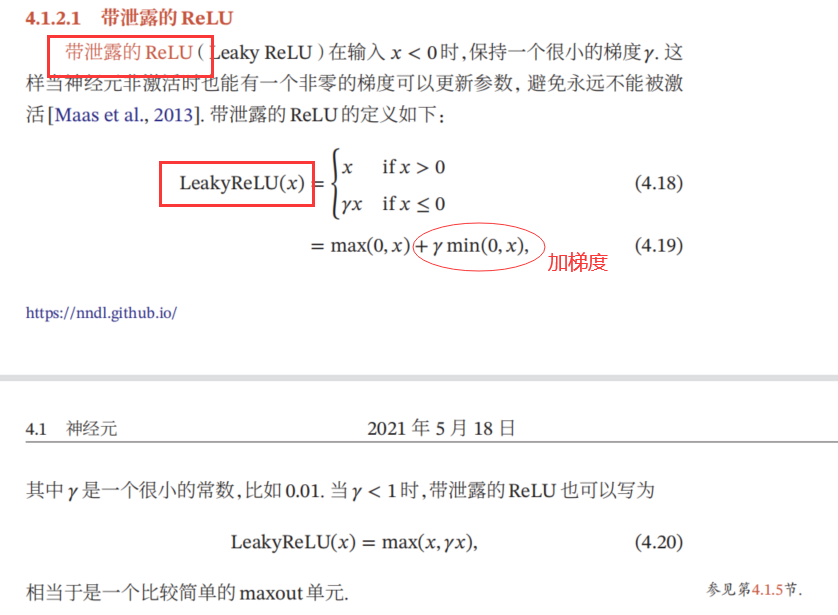
带参数的ReLU

ELU函数

Softplus函数

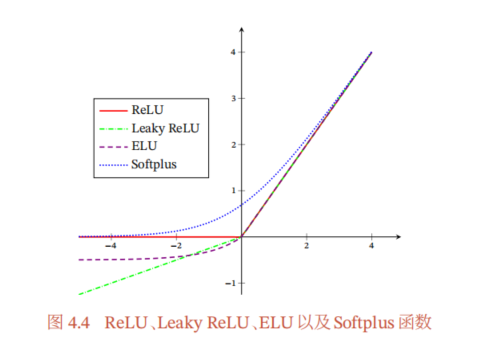
四种函数图对比:
Swish函数
1
2
| 1.自门控激活函数
2.通过设置得到1/0 --> 门的状态为"开"/"关"
|

GELU函数
1
2
| 1.高斯误差线性单元 --> 通过门控机制来调整其输出值的激活函数
2.特殊的Swish函数
|

Maxout单元

网络结构
三种网络结构:
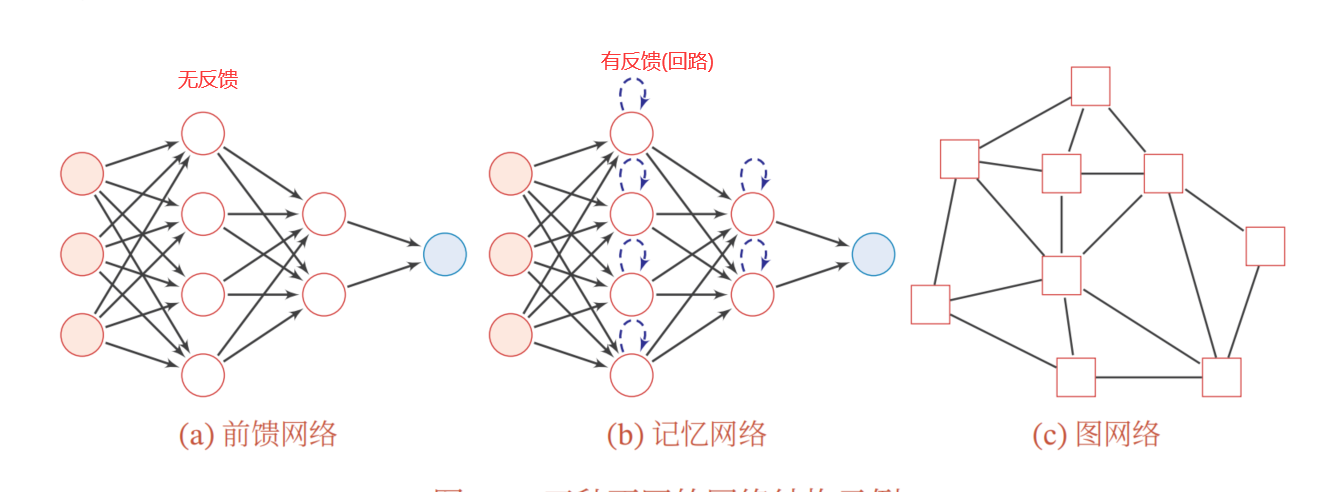
前馈神经网络
反向传播算法
##



















