1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
| import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
from sklearn.preprocessing import MinMaxScaler #归一化
from scipy import stats
from sklearn.decomposition import PCA #PCA主成分降维
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression #线性回归
from sklearn.neighbors import KNeighborsRegressor #K近邻回归
from sklearn.tree import DecisionTreeRegressor #决策树回归
from sklearn.ensemble import RandomForestRegressor #随机森林回归
from sklearn.svm import SVR # 支持向量回归
import lightgbm as lgb # LightGBM模型
from sklearn.model_selection import train_test_split # 切分数据
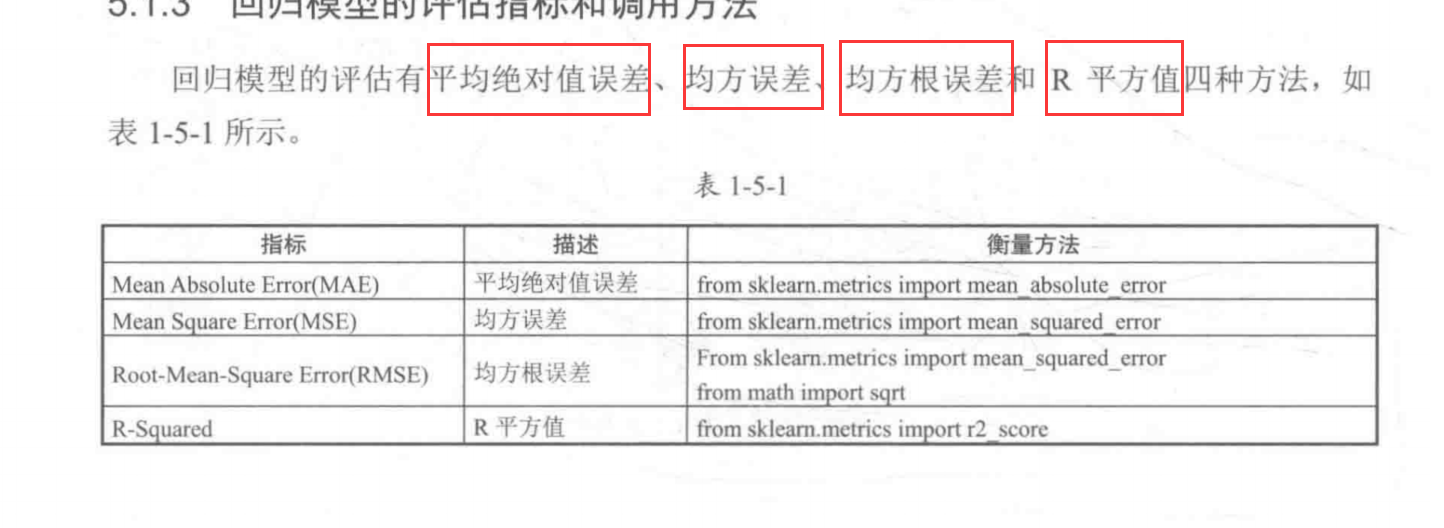
from sklearn.metrics import mean_squared_error #均方误差
from sklearn.metrics import mean_absolute_error #平均绝对值误差
from math import sqrt #平方根
from sklearn.metrics import r2_score #R平方值
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
from sklearn.pipeline import Pipeline #管道
from sklearn.preprocessing import PolynomialFeatures #多项式转变
from sklearn.preprocessing import StandardScaler #标准化
from sklearn.linear_model import SGDRegressor #随机递推下降
from sklearn.model_selection import KFold #KFold是K折交叉验证
from sklearn.model_selection import LeaveOneOut #留一法
from sklearn.model_selection import LeavePOut #留P法
#1.读取数据
train_data_file = "zhengqi_train.txt"
test_data_file = "zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8') #训练集数据共有2888个样本(V0-V37共38个特征变量) -- 有target字段
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8') #测试集数据共有1925个样本(V0-V37共有38个特征变量) -- 无target字段
#2.归一化(最大值和最小值) --放缩到(0,1区间)
features_columns=[col for col in train_data.columns if col not in ['target']] #从V0到V37
min_max_scaler=preprocessing.MinMaxScaler().fit(train_data[features_columns])
train_data_scaler=min_max_scaler.transform(train_data[features_columns])
test_data_scaler=min_max_scaler.transform(test_data[features_columns])
train_data_scaler=pd.DataFrame(train_data_scaler) #将训练集数据弄成DF格式
train_data_scaler.columns=features_columns
test_data_scaler=pd.DataFrame(test_data_scaler) #将测试集数据弄成DF格式
test_data_scaler.columns=features_columns
train_data_scaler['target'] = train_data['target']
#3.PCA处理
### 1.sklearn.decomposition.PCA PCA处理之后可保持90%的信息数据
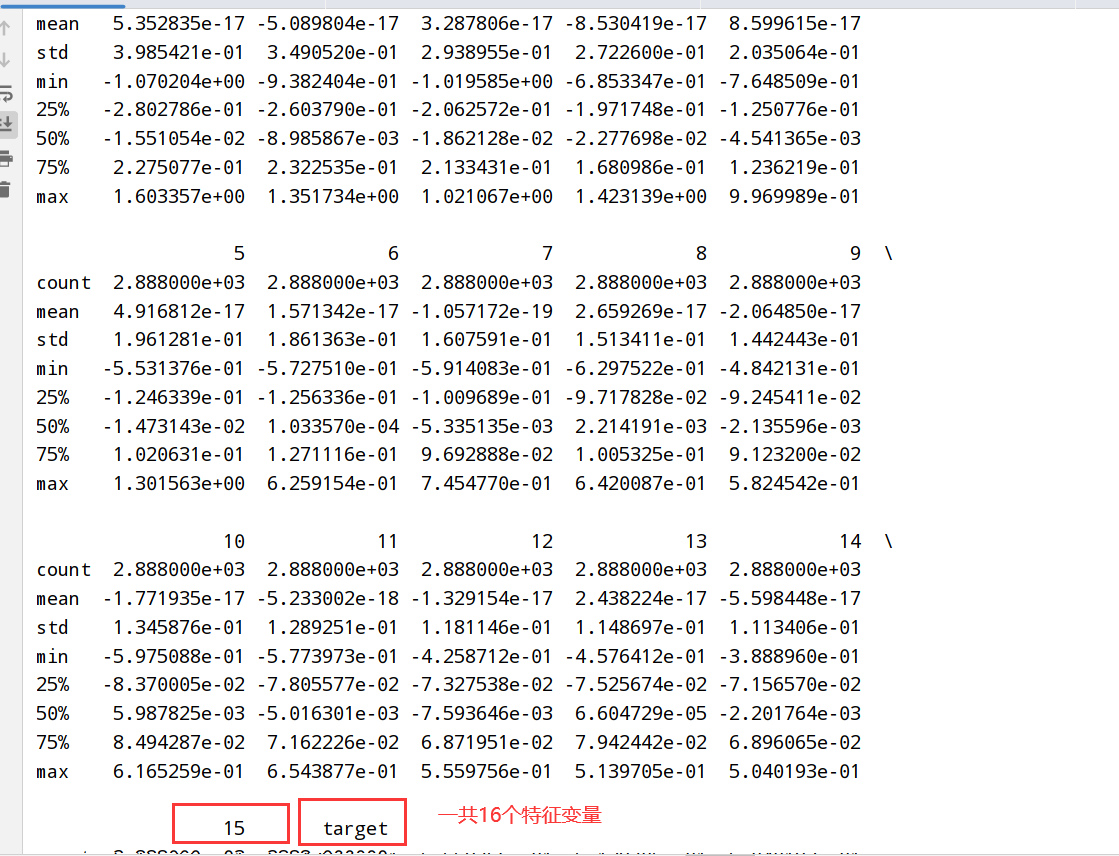
pca=PCA(n_components=16) # 整数表示保留几个特征 小数表示百分之多少的信息
#获得转换器
new_train_pca_16=pca.fit_transform(train_data_scaler.iloc[:,0:-1])
new_test_pca_16=pca.transform(test_data_scaler)
#转移为DF格式
new_train_pca_16=pd.DataFrame(new_train_pca_16)
new_test_pca_16=pd.DataFrame(new_test_pca_16)
new_train_pca_16['target']=train_data_scaler['target'] # PCA处理之后保留了16个主成分
#4.切分数据(训练集--> 80%训练集和20%验证数据)
new_train_pca_16=new_train_pca_16.fillna(0) #采用PCA保留16维特征的数据
train=new_train_pca_16[new_test_pca_16.columns]
target=new_train_pca_16['target']
##切分数据 训练数据80% 验证数据20%
train_data,test_data,train_target,test_target=train_test_split(train,target,test_size=0.2,random_state=0)
#5.模型交叉验证
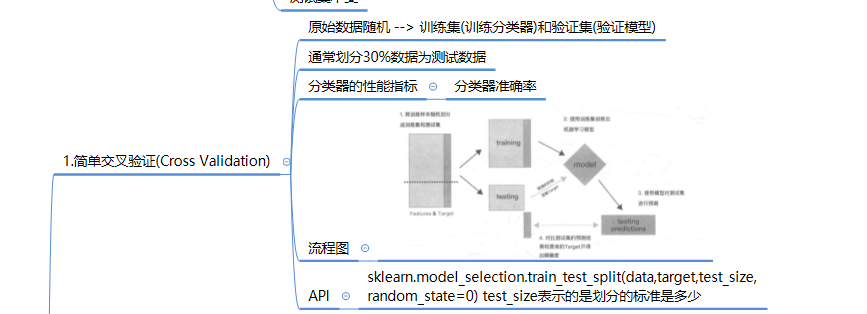
##5.1 简单交叉验证
clf=SGDRegressor(max_iter=1000,tol=1e-3) # max_iter表示是训练数据的最大传递次数 tol是停止标准
clf.fit(train_data,train_target) #装在转换器
score_train = mean_squared_error(train_target, clf.predict(train_data))
score_test = mean_squared_error(test_target, clf.predict(test_data))
#print("SGDRegressor train MSE:",score_train) # SGDRegressor train MSE: 0.1415415271798254
#print("SGDRegressor test MSE:",score_test) # SGDRegressor test MSE: 0.147046507243961
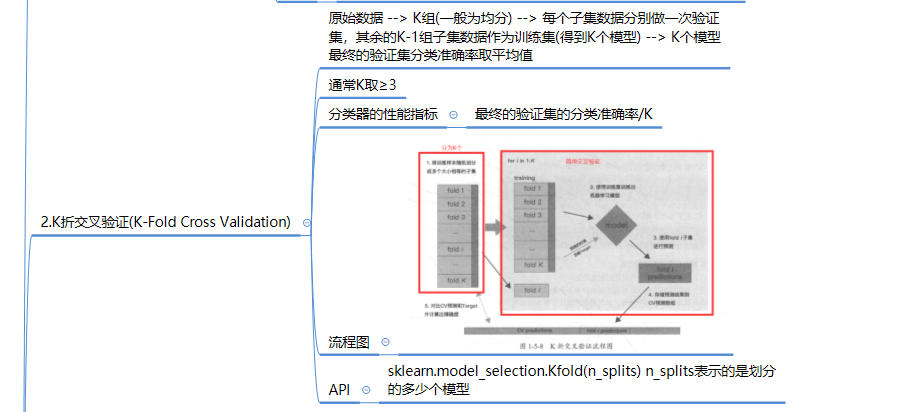
##5.2 k折交叉验证
kf=KFold(n_splits=5)
for k,(train_index,test_index) in enumerate(kf.split(train)):
train_data,test_data,train_target,test_target=train.values[train_index],train.values[test_index],target[train_index],target[test_index]
clf = SGDRegressor(max_iter=1000,tol=1e-3) # max_iter表示是训练数据的最大传递次数 tol是停止标准
clf.fit(train_data,train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data))
score_test = mean_squared_error(test_target, clf.predict(test_data))
print(k,"折","SGDRegressor train MSE:",score_train) # x 折 SGDRegressor train MSE: 0.1415415271798254
print(k,"折","SGDRegressor test MSE:",score_test) # x 折 SGDRegressor train MSE: 0.1415415271798254
##5.3 留一法 LOO CV
loo=LeaveOneOut()
num=100
for k,(train_index,test_index) in enumerate(loo.split(train)):
train_data,test_data,train_target,test_target = train.values[train_index],train.values[test_index],target[train_index],target[test_index]
clf = SGDRegressor(max_iter=1000,tol=1e-3) # max_iter表示是训练数据的最大传递次数 tol是停止标准
clf.fit(train_data,train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data))
score_test = mean_squared_error(test_target, clf.predict(test_data))
print(k,"个","SGDRegressor train MSE:",score_train)
print(k,"个","SGDRegressor test MSE:",score_test)
if k >= 9:
break
##5.4 留P法 LPO CV
lpo=LeavePOut(p=10)
num=100
for k,(train_index, test_index) in enumerate(lpo.split(train)):
train_data,test_data,train_target,test_target = train.values[train_index],train.values[test_index],target[train_index],target[test_index]
clf = SGDRegressor(max_iter=1000,tol=1e-3) # max_iter表示是训练数据的最大传递次数 tol是停止标准
clf.fit(train_data, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data))
score_test = mean_squared_error(test_target, clf.predict(test_data))
print(k,"10个","SGDRegressor train MSE:",score_train)
print(k,"10个","SGDRegressor test MSE:",score_test)
if k >= 9:
break
|