验证回文数(双指针/API翻转方法) 题目
分析 1. 双指针法:先用stringbuilder筛选出只有字符和数字的字符串,然后进行两端双指针移动判断。
2. API翻转函数:先用stringbuilder筛选出只有字符和数字的字符串,字符串翻转API得到sgood的逆序字符串。代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 public class HuiWen { public static void main(String[] args) { Scanner input = new Scanner(System.in); String s=input.nextLine(); //可以输入空格 System.out.println(isPalindrome(s)); } public static boolean isPalindrome(String s) { StringBuilder sb=new StringBuilder(); int len=s.length(); for(int i=0;i<len;i++){ if(s.charAt(i)>='0'&&s.charAt(i)<='9'||s.charAt(i)>='a'&&s.charAt(i)<='z'){ sb.append(s.charAt(i)); } if(s.charAt(i)>='A'&&s.charAt(i)<='Z'){ sb.append((char)(s.charAt(i)+32)); } } int left=0; int right=sb.length()-1; while(left<right){ if(sb.charAt(left)==sb.charAt(right)){ left++; right--; }else{ return false; } } return true; } public static boolean isPalindromeer(String s) { StringBuilder sb=new StringBuilder(); int len=s.length(); for(int i=0;i<len;i++){ char ch=s.charAt(i); if(Character.isLetterOrDigit(ch)){ sb.append(Character.toLowerCase(ch)); } } StringBuilder sbfan=new StringBuilder(sb).reverse(); return sb.toString().equals(sbfan.toString()); } }
结果
两数相加(预设pre头链表) 题目
分析
参考大佬思路:
https://leetcode-cn.com/problems/add-two-numbers/solution/hua-jie-suan-fa-2-liang-shu-xiang-jia-by-guanpengc/
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 public static ListNode addTwoNumbers(ListNode l1, ListNode l2) { ListNode pre=new ListNode(0); ListNode cur=pre; //cur是当前pre位置 int carry=0; while(l1!=null||l2!=null){ int x = l1 == null ? 0 : l1.val; //计算l1当前节点的值 int y = l2 == null ? 0 : l2.val; //计算l2当前节点的值 int sum=x+y+carry; //计算总和 carry=sum/10; //carry代表进位 sum=sum%10; //当前位置应该放的数字 cur.next=new ListNode(sum); //当前节点的后面节点的值是sum cur=cur.next; //往后移动 if(l1 != null) { l1 = l1.next; } if(l2 != null) { l2 = l2.next; } if(carry == 1) { //有进位就下一个节点给这个进位 到时候会反序输出 cur.next = new ListNode(carry); } } return pre.next; //cur一直移动到新链表的尾 pre.next返回新链表的第一个节点 } }
结果
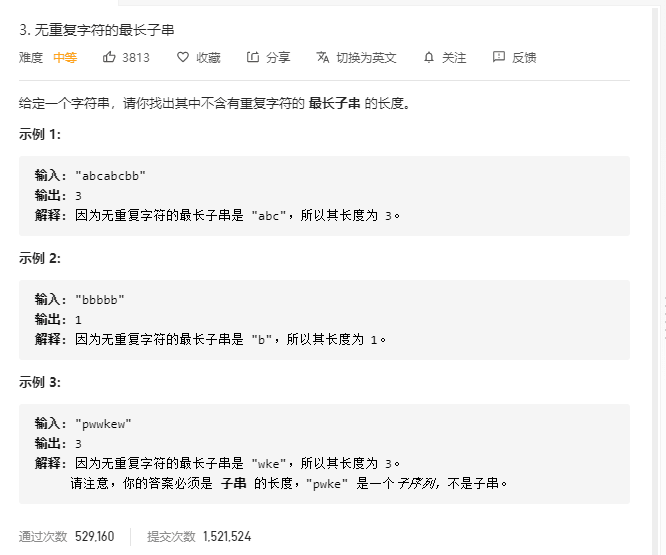
无重复字符的最长子串(map集合) 题目
分析 1.使用map集合不断存放当前值和所在字符的下标位置,然后不断更新ans结果值。代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public class WuChongFuZiChuan { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s=input.next(); System.out.println(lengthOfLongestSubstring(s)); } public static int lengthOfLongestSubstring(String s) { int n = s.length(); //获取字符串长度 int ans = 0; Map<Character, Integer> map = new HashMap<>(); int start=0; for (int end = 0; end < n; end++) { char a = s.charAt(end); //获取当前位置字符 if (map.containsKey(a)) { start = Math.max(map.get(a), start); } ans = Math.max(ans, end - start + 1); //算距离 map.put(s.charAt(end), end + 1); //当前map里面存当前字符串字符和下标 } return ans ; } }
结果
寻找两个正序数组的中位数(新建arr) 题目
分析 1. 新建数组遍历将a和b数组内容存放进去
2. 然后Arrays.sort()方法排序
3. 排序之后判断奇偶性之后就可以找中位数代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public class ZhongWeiShu { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int m=input.nextInt(); int[] a=new int[n]; int[] b=new int[m]; for(int i=0;i<n;i++){ a[i]=input.nextInt(); } for(int i=0;i<m;i++){ b[i]=input.nextInt(); } System.out.println(findMedianSortedArrays(a,b)); } public static double findMedianSortedArrays(int[] nums1, int[] nums2) { int n=nums1.length; int m=nums2.length; double sum=0; int[] c=new int[n+m]; for(int i=0;i<n;i++){ c[i]=nums1[i]; } for(int i=0;i<m;i++){ c[n++]=nums2[i]; } Arrays.sort(c); //进行排序 //字符串形式输出检验是否正确 //System.out.println(Arrays.toString(c)); //判断奇偶性找中位数 if(c.length%2==0){ sum=(c[c.length/2]+c[c.length/2-1])/2.0; }else{ sum=c[c.length/2]; } return sum; } }
结果
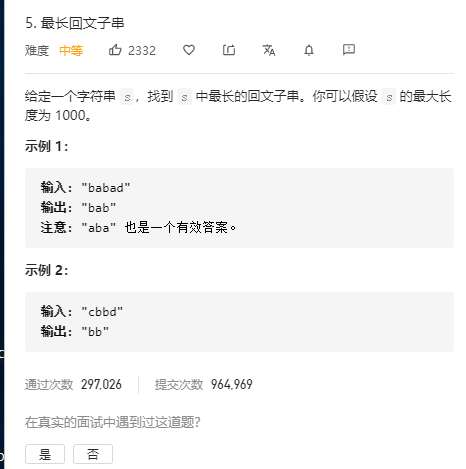
最长回文子串(暴力/动规/马拉车) 题目
分析 1.暴力法:两层循环遍历字符串得到子串然后进行判断
2.动态规划:新建dp[N][N]布尔数组判断i到j是否是回文,要让dp[i][j]满足条件,就要是dp[i+1][j-1]也满足条件的基础上动态推进
3.马拉车:不太实用其他算法代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 public class MaxString { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s=input.next(); System.out.println(longestPalindrome(s)); } //1.暴力遍历每个子串判断 public static String longestPalindrome(String s) { //s为空字符串就输出本身(null) if(s.isEmpty()){ return s; } //获取s的前两个 String res=s.substring(0,1); //二重循环暴力遍历每个子串 for (int i = 0; i < s.length(); i++) { for (int j = i + 1; j <= s.length(); j++) { String t=s.substring(i,j); String tf=new StringBuilder(t).reverse().toString(); if(t.equals(tf)&&t.length()>res.length()){ res=t; } } } return res; } //2.动态规划 private static String longestPalindromer(String s) { //如果字符串为空就返回自己(null) if (s.isEmpty()) { return s; } int n = s.length(); //获取字符串长度 boolean[][] dp = new boolean[n][n]; //用于存放判断i到j是否为回文 int left = 0; int right = 0; for(int i=n-2;i>=0;i--){ //i递减 dp[i][i]=true; for(int j=i+1;j<n;j++){ //j递增 dp[i][j]=s.charAt(i)==s.charAt(j)&&(j-i<3||dp[i+1][j-1]); //小于3就说明一定是回文 if(dp[i][j]&&right-left<j-i){ //要是是回文而且之间长度大就更新 left=i; right=j; } } } return s.substring(left,right+1); //返回 } }
结果
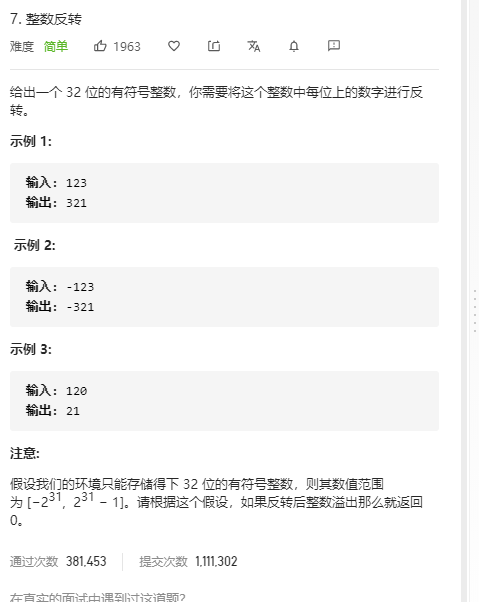
整数反转(字符串反转/除10换) 题目
分析 1. 可以拆数/10存数组输出
2. 数字转字符串之后反转然后转整数输出(异常捕获!!!!!!!!!!)代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public class FanZhuan { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); System.out.println(reverse(n)); } public static int reverse(int n) { int res=0; //最后结果 String temp=""; //整数转字符串 反转之后的结果 if(n>0){ temp=new StringBuilder(String.valueOf(n)).reverse().toString(); }else{ temp="-"+new StringBuilder(String.valueOf(n).substring(1)).reverse().toString(); //从第二个位置开始 第一个是-号 } if(temp.equals("")){ temp = "0"; //n为0 } //异常捕捉 try{ res= Integer.valueOf(temp); //字符串反转之后转整数int } catch(Exception ex){ return 0; } return res; } }
结果
字符串转整数(atoi) 题目
分析
大佬思路:
https://leetcode-cn.com/problems/string-to-integer-atoi/solution/java-zi-fu-chuan-zhuan-zheng-shu-hao-dong-by-sweet/
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 public class FanZhuan { public static void main(String[] args) { Scanner input=new Scanner(System.in); String str=input.nextLine(); System.out.println(myAtoi(str)); } public static int myAtoi(String str) { char[] chars = str.toCharArray(); //字符串转字符数组 int n = chars.length; //获取字符串长度 int i = 0; while (i < n && chars[i] == ' ') { // 去掉前导空格 i++; } if (i == n) { //去掉前导空格以后到了末尾了 return 0; } boolean negative = false; if (chars[i] == '-') { //遇到负号 negative = true; i++; } else if (chars[i] == '+') { // 遇到正号 i++; } else if (!Character.isDigit(chars[i])) { // 其他符号 return 0; } int ans = 0; while (i < n && Character.isDigit(chars[i])) { //数字范围内 int digit = chars[i] - '0'; if (ans > (Integer.MAX_VALUE - digit) / 10) { // 本来应该是 ans * 10 + digit > Integer.MAX_VALUE // 但是 *10 和 + digit 都有可能越界,所有都移动到右边去就可以了。 return negative? Integer.MIN_VALUE : Integer.MAX_VALUE; } ans = ans * 10 + digit; //其余成功的情况下直接得到目前的值 i++; //下标后移判断下一位 } return negative? -ans : ans; //看是正数还是负数 } }
结果
罗马数字转整数(分类) 题目
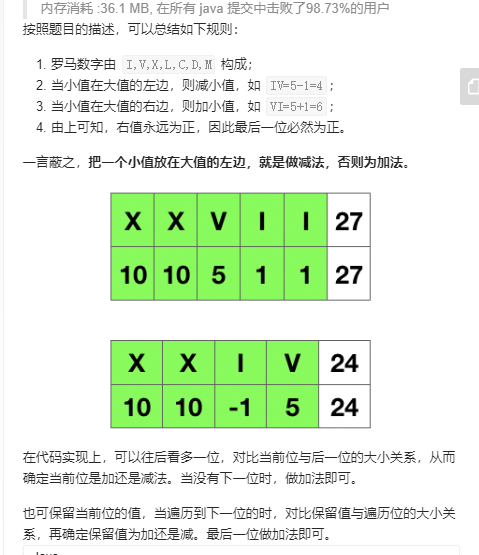
分析
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution { public int romanToInt(String s) { int sum = 0; int preNum = getValue(s.charAt(0)); for(int i = 1;i < s.length(); i ++) { int num = getValue(s.charAt(i)); if(preNum < num) { sum -= preNum; } else { sum += preNum; } preNum = num; } sum += preNum; return sum; } private int getValue(char ch) { switch(ch) { case 'I': return 1; case 'V': return 5; case 'X': return 10; case 'L': return 50; case 'C': return 100; case 'D': return 500; case 'M': return 1000; default: return 0; } } }
结果
最长公共前缀(一个比多个) 题目
分析
大佬思路:
https://leetcode-cn.com/problems/longest-common-prefix/solution/14ti-zui-chang-gong-gong-qian-zhui-by-iceblood/
(1) 取数组中一个字符串从前往后遍历字符去匹配其它字符串的相同位置字符。
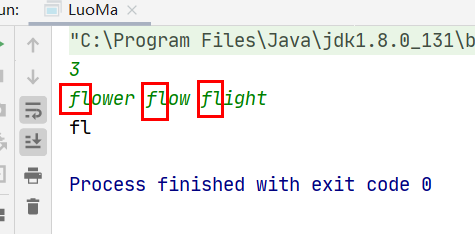
(2) 直到遍历超出数组中最短字符串长度或者遍历到的字符匹配不上,则返回当前匹配串。代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public class LuoMa { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); String[] strs=new String[n]; for(int i=0;i<n;i++){ strs[i]=input.next(); } System.out.println(longestCommonPrefix(strs)); } public static String longestCommonPrefix(String[] strs) { if (strs == null || strs.length == 0) { return ""; } for (int i=0;i<strs[0].length();i++) { char c=strs[0].charAt(i); //取出当前位置要匹配的所有字符 for (int j=1;j<strs.length;j++) { //字符数组后面的每个字符串 if(i==strs[j].length()||strs[j].charAt(i)!=c){ return strs[0].substring(0,i); //只返回第一个字符串的到i的值 } } } // 数组中其它字符串都能被 strs[0] 匹配。 return strs[0]; } }
结果
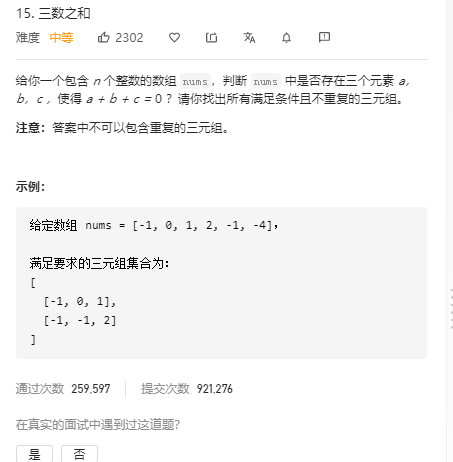
三数之和(集合嵌套) 题目
分析
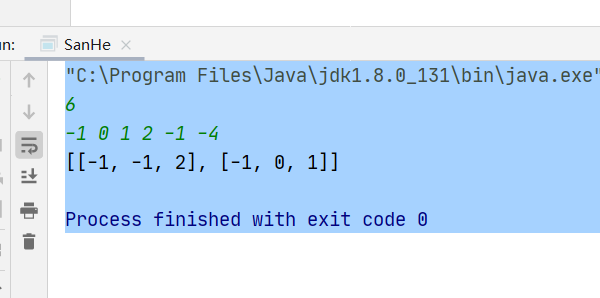
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 public class SanHe { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] nums=new int[n]; for(int i=0;i<n;i++){ nums[i]=input.nextInt(); } System.out.println(threeSum(nums)); } public static List<List<Integer>> threeSum(int[] nums) { List<List<Integer>> ans=new ArrayList<>(); //最终结果 int len=nums.length; if(nums == null || len < 3) { //如果长度小于3就输出ans return ans; } Arrays.sort(nums); //数组排序之后递增 for(int i =0;i<len;i++){ if(nums[i] > 0) { break; // 如果当前数字大于0,则三数之和一定大于0,所以结束循环 } if(i > 0 && nums[i] == nums[i-1]) { continue; // 去重 } int L = i+1; int R = len-1; while(L < R){ int sum = nums[i] + nums[L] + nums[R]; if(sum == 0){ ans.add(Arrays.asList(nums[i],nums[L],nums[R])); while (L<R && nums[L] == nums[L+1]) { L++; // 去重 } while (L<R && nums[R] == nums[R-1]) { R--; // 去重 } L++; R--; } else if (sum < 0) { //要在右边找厉害的 L++; } else if (sum > 0) { //要在左边找厉害的 R--; } } } return ans; } }
结果
电话号码组合(回溯) 题目
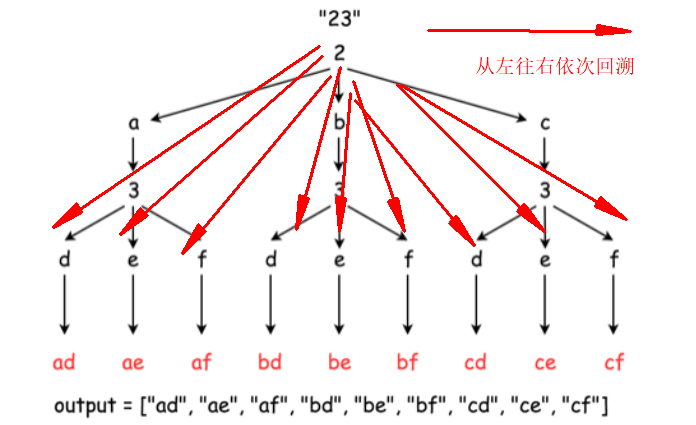
分析 其实就是将号码存到一个map集合,然后以23为例,将2的所有对应字符串字符遍历。每次都拿出来一个去深度找i+1位置的3的对应值
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 public class TempZUhe { public static void main(String[] args) { Scanner input=new Scanner(System.in); String digits=input.next(); System.out.println(letterCombinations(digits)); } public static List<String> letterCombinations(String digits) { if (digits == null || digits.length() == 0) { //字符串为空或者不存在 return new ArrayList(); } Map<Character, String> map = new HashMap<Character, String>(); map.put('2', "abc"); //对应数字对应的字符串 map.put('3', "def"); map.put('4', "ghi"); map.put('5', "jkl"); map.put('6', "mno"); map.put('7', "pqrs"); map.put('8', "tuv"); map.put('9', "wxyz"); List<String> res = new LinkedList<String>(); //保存最终结果 helper("", digits, 0, res, map); //新建helper方法添加 return res; } private static void helper(String s, String digits, int i, List<String> res, Map<Character, String> map) { if (i == digits.length()) { res.add(s); //如果传入的当前下表是最后一个 return; //结果添加空 } String letters = map.get(digits.charAt(i)); //获取当前位置的对应字符串 2找abc for (int j = 0; j < letters.length(); j++){ //依次将a b c 放入 //原来基础上加上现在的字符串下标 helper(s+letters.charAt(j),digits,i+1,res,map); //i+1是回溯找23的 ad ae af } } }
结果
有效的括号(栈/指针移动匹配) 题目
分析 思路:
遇到左括号就右移
遇到右括号先左移然后判断是否匹配代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 public class KuoHaoKmp { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s=input.next(); System.out.println(isValid(s)); } public static boolean isValid(String s) { if(s.length()%2!=0){ //字符串长度是奇数 肯定错误 return false; } if(s.length()==0){ //字符串长度为空 肯定正确 return true; } char[] charArray=new char[s.length()+1]; int flag=1; for(char c:s.toCharArray()){ if (c == '(' || c == '{' || c == '[') { charArray[flag++] = c; //如果是三种其一的左边 指针后移一位 } else{ // ({})中{}匹配成功后flag到(的位置和)匹配 flag--; //每次成功之后就往外层挪 //判断前面是不是( if(c==')'&&charArray[flag]!='('){ return false; } //判断前面是不是{ if (c == '}' && charArray[flag] != '{') { return false; } //判断前面是不是[ if (c == ']' && charArray[flag] != '[') { return false; } } } return flag==1;// 左括号还有剩余 (匹配成功会flag还是1) } }
结果
括号生成(回溯) 题目
分析 1. 利用res集合存结果,字符串存每一次的可能
2. 生成可能:
左边还可以添加的条件:左边还有
右边还可以添加的条件: 左边剩余<右边剩余代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public class ShengKuoHao { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); System.out.println(generateParenthesis(n)); } public static List<String> generateParenthesis(int n) { List<String> res=new ArrayList<>(); if (n == 0) { return res; //长度为0返回空 } // 执行深度优先遍历,搜索可能的结果 dfs("", n, n, res); return res; } private static void dfs(String s, int n, int n1, List<String> res) { if(n==0&&n1==0){ //左右都没有可以用的 res.add(s); //将s字符串存入结果 return; } if(n>n1){ return; //左边剩下的多余右边剩下的 错误 } if(n>0){ dfs(s+"(",n-1,n1,res); //左边还可以添加 } if(n1>0){ dfs(s+")",n,n1-1,res); //右边还可以添加 } } }
结果
实现strStr()函数(使用substring()方法) 题目
分析 1. 找到最后一位 -- 结果=最后一位-needle长度+1
2. 使用substring(x,y)找子串然后返回x的下标代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public class strStr { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s1=input.next(); String s2=input.next(); System.out.println(strStrer(s1,s2)); } public static int strStrer(String haystack, String needle) { int len=haystack.length(); int er=needle.length(); if(needle.length()==0){ return 0; //needle为空返回0 } if(haystack.length()==0){ return -1; //haystack为空返回-1 } for(int i=0;i<len-er+1;i++){ if(haystack.substring(i,i+er).equals(needle)){ return i; //找到就返回i } } return -1; //找不到返回-1 } }
结果
两数相除(考虑正负情况) 题目
分析 采用二分法的思想,dividend每次减去2^n个divisor(尽可能多),同时reslut每次加2^n代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { public int divide(int dividend, int divisor) { if(dividend==Integer.MIN_VALUE&&divisor==-1) return Integer.MAX_VALUE; //判断是否是负数 boolean k=(dividend>0&&divisor>0)||(dividend<0&&divisor<0); int result=0; dividend=-Math.abs(dividend); divisor=-Math.abs(divisor); while(dividend<=divisor) { int temp=divisor; int c=1; while(dividend-temp<=temp) { temp=temp<<1; c=c<<1; } dividend-=temp; result+=c; } return k?result:-result; } }
结果
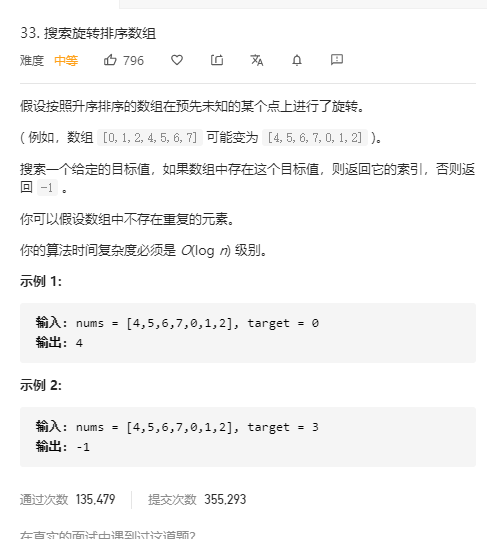
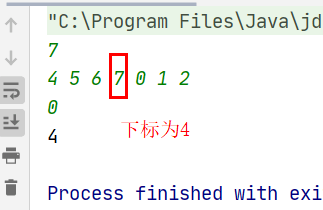
搜索旋转排序数组(二分法/暴力法) 题目
分析
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 public static int search(int[] nums, int target) { int left=0; //左指针 int right=nums.length-1; //右指针 int mid=0; //中间指针 while (left<=right) { mid=left+(right-left)/2; //找中间值(二分法) if(nums[mid]==target){ return mid; //找到返回下标 } //判断mid是在左端 if(nums[left]<=nums[mid]){ // 2 5 //判断target在mid左边还是右边 if(target>=nums[left]&&target<nums[mid]){ //target是4 right=mid-1; }else { //target是 left=mid+1; } } //判断mid是在右端 else{ if(target>nums[mid]&&target<=nums[right]){ left=mid+1; }else { right=mid-1; } } } return -1; }
结果
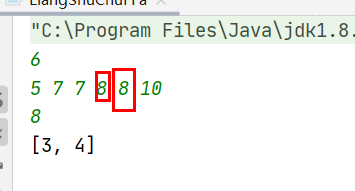
数组元素初始和结束为止(二分法/正反序查找) 题目
分析 1. 正序找初始位置反序找结束位置代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public class LiangShuChuFFa { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++){ a[i]=input.nextInt(); } int target=input.nextInt(); System.out.println(Arrays.toString(searchRange(a,target))); } public static int[] searchRange(int[] nums, int target) { int[] a=new int[]{-1,-1}; //默认找不到的-1 -1 int len=nums.length; //正序找到初始点 for(int i=0;i<len;i++){ if(nums[i]==target){ a[0]=i; //第一次出现位置 break; } } //反序找到最终点 for(int i=len-1;i>=0;i--){ if(nums[i]==target){ a[1]=i; //最后一次出现位置 break; } } return a; } }
结果
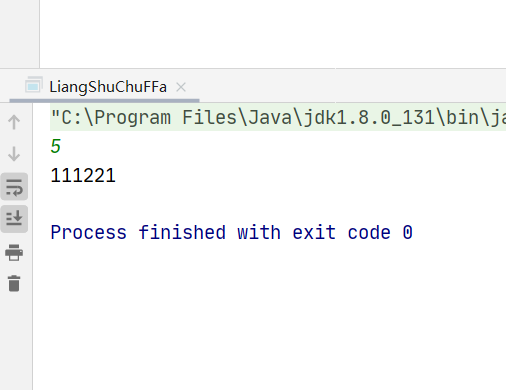
外观数列(递归) 题目
分析 1. 其实就是每次将前面的数字串计算每一位不同的数字出现的次数是多少.
2.举例:n==5的时候就是描述4时候的1211:
1个1/1个2/2个1 --> 11 12 21 --> 111221
3. 思路:
3.1 其实就是不断递归找前面的结果推后面的结果
3.2 不断的使用stringbuiler添加数字和个数然后往后推代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public class LiangShuChuFFa { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); System.out.println(countAndSay(n)); } public static String countAndSay(int n) { String res = "1"; for (int i = 2; i <= n; i++) { StringBuilder temp = new StringBuilder(); for (int j = 0; j <res.length(); j++) { int count = 1; while (j + 1 < res.length() && res.charAt(j) == res.charAt(j + 1)) { //j+1小心越界 count++; //记录出现几次 j++; //下标更新 } temp.append(count).append(res.charAt(j)); //添加某个数出现了多少次 2次2 3次4等等 } res = temp.toString(); //res接上一次的结果 } return res; } }
结果
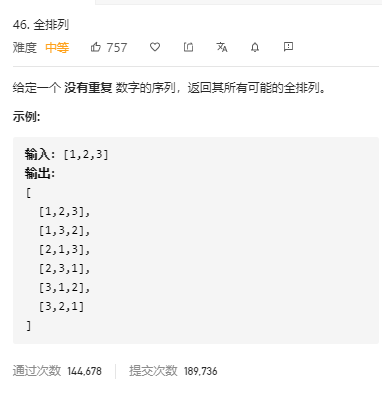
全排列(回溯/dfs) 题目
分析 https://leetcode-cn.com/problems/permutations/solution/quan-pai-lie-by-leetcode-solution-2/
布尔数组used识别是否使用过
path栈存放每一次的路径(每一次更改used属性存入栈顶然后dfs方法,移除更改属性)
res集合嵌套存放结果(每次新建list存入最终的list集合嵌套)代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 public class LiangShuChuFFa { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++){ a[i]=input.nextInt(); } System.out.println(permute(a)); } public static List<List<Integer>> permute(int[] nums) { int len=nums.length; //获取数组长度 List<List<Integer>> res=new ArrayList<>(); if(len==0){ return res; //长度为0返回空 } Deque<Integer> path=new ArrayDeque<>(); //栈用于存每次的回溯结果 boolean[] used=new boolean[len]; //used数组用于判断每位是否使用过 dfs(nums,len,0,path,used,res); //调用方法 return res; //返回结果 } private static void dfs(int[] nums, int len, int depth, Deque<Integer> path, boolean[] used, List<List<Integer>> res) { //终止条件!!!! if(depth==len){ //回溯的高度和数字长度一样就说明到底了 res.add(new ArrayList<>(path)); //结果新建一个list集合添加进去 return; //返回空 void } for(int i=0;i<len;i++){ if(used[i]==true){ continue; //使用过跳过这段 } path.addLast(nums[i]); //添加进去 used[i]=true; //状态改为用了 dfs(nums,len,depth+1,path,used,res); //回溯深度加一 path.removeLast(); //移除刚才那个 used[i]=false; //状态又改为未用过 } } }
结果
旋转图像(找规律更换) 题目
分析 https://leetcode-cn.com/problems/rotate-image/solution/yi-ci-xing-jiao-huan-by-powcai/
(i,j),(j, n-i-1),(n-i-1, n-j-1),(n -j-1, i)这四个索引号上的数交换。代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public class LiangShuChuFFa { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[][] a=new int[n][n]; for(int i=0;i<n;i++){ for(int j=0;j<n;j++){ a[i][j]=input.nextInt(); } } rotate(a); for(int i=0;i<n;i++){ for(int j=0;j<n;j++){ System.out.print(a[i][j]); } System.out.println(); } } public static void rotate(int[][] matrix) { int n = matrix.length; for (int i = 0; i < n/2; i++ ) { for (int j = i; j < n - i - 1; j ++ ){ int tmp = matrix[i][j]; matrix[i][j] = matrix[n-j-1][i]; matrix[n-j-1][i] = matrix[n-i-1][n-j-1]; matrix[n-i-1][n-j-1] = matrix[j][n-i-1]; matrix[j][n-i-1] = tmp; } } } }
结果
字母异位词分组(map的key映射value) 题目
分析 1. 思路:使用对每一个字符数组的元素就是一个字符串进行排序之后将其设置成一个key值,然后通过map集合映射,最后每次生成一个list集合输出即可代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 public class LiangShuChuFFa { public static void main(String[] args) { Scanner input=new Scanner(System.in); String[] a=new String[]{"eat", "tea", "tan", "ate", "nat", "bat"}; System.out.println(groupAnagrams(a)); } public static List<List<String>> groupAnagrams(String[] strs) { HashMap<String, List<String>> hash = new HashMap<>(); for(int i=0;i<strs.length;i++){ char[] arr=strs[i].toCharArray(); //每一个字符串都转为一个字符数组 //1. 排序 Arrays.sort(arr); //2. 映射到key String key=String.valueOf(arr); //获取数组的值 if(hash.containsKey(key)){ hash.get(key).add(strs[i]); //这个值添加那个字符串 } //2. 没有这个key 新建一个map存入这个 else{ List<String> temp = new ArrayList<String>(); temp.add(strs[i]); //temp里面添加这个字符串 hash.put(key,temp); //map存放这个字符串和key } } return new ArrayList<>(hash.values()); //新建list集合每次输出一个key的value们 } }
结果
螺旋矩阵(四指针判断) 题目
分析 代码 1 2 3 4 5 class Solution { public List<Integer> spiralOrder(int[][] matrix) { } }
结果
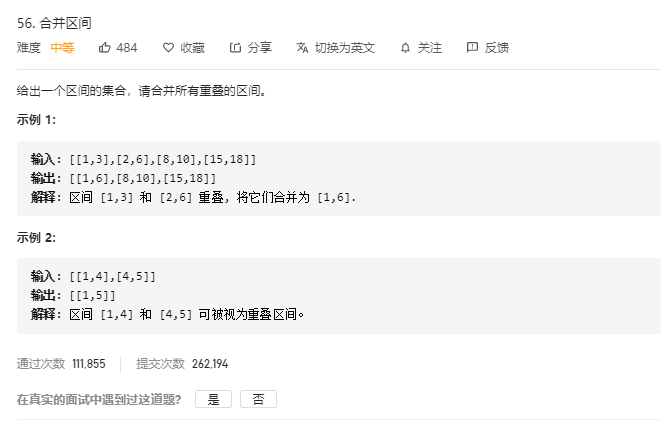
合并区间(集合) 题目
分析 其实只要关注每一行的首位和中间位置的不同,是否可以合并就行代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public int[][] merge(int[][] intervals) { // 先按照区间起始位置排序 Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]); // 遍历区间 int[][] res = new int[intervals.length][2]; int idx = -1; for (int[] interval: intervals) { // 如果结果数组是空的,或者当前区间的起始位置 > 结果数组中最后区间的终止位置, // 则不合并,直接将当前区间加入结果数组。 if (idx == -1 || interval[0] > res[idx][1]) { res[++idx] = interval; } else { // 反之将当前区间合并至结果数组的最后区间 res[idx][1] = Math.max(res[idx][1], interval[1]); } } return Arrays.copyOf(res, idx + 1); } }
结果
跳跃游戏(贪心) 题目
分析 1. 思路:for循环遍历所有的数组成员
2. 不断地更新迭代找rightmost的最大值就是右边能跳多远,如果能跳的距离比数组长度大的话一定可以到达true代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int j=0;j<n;j++){ a[j]=input.nextInt(); } System.out.println(canJump(a)); } public static boolean canJump(int[] nums) { int n=nums.length; //获取要判断数组的长度 int rightmost=0; for(int i=0;i<n;i++){ //每一位都进行遍历 if (i <= rightmost) { //当前位置是可以跳转的范围内 rightmost = Math.max(rightmost, i + nums[i]); //右边能跳的距离为最大 if (rightmost >= n - 1) { return true; //如果能跳的距离比数组长度大 就一定可以true } } } return false; } }
结果
加一(进位问题) 题目
分析 1. 末位无进位,则末位加一即可,因为末位无进位,前面也不可能产生进位,比如 45 => 46
2. 末位有进位,在中间位置进位停止,则需要找到进位的典型标志,即为当前位 %10 后为 0,则前一位加 1,直到不为 0 为止,比如 499 => 500
3. 末位有进位,并且一直进位到最前方导致结果多出一位,对于这种情况,需要在第 2 种情况遍历结束的基础上,进行单独处理,比如 999 => 1000代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 public int[] plusOne(int[] digits) { int n = digits.length; for(int i = n -1;i>=0;i--){ //倒序 if(digits[i] == 9){ digits[i] = 0; //如果当前位置是9 就要变为0 }else{ digits[i]++; //其他数字就直接+1 return digits; //然后返回 } } int[] a = new int [n+1]; //新建数组a存放结果 a[0]=1; //给999这+1增加进位留一位为1 return a; }
结果
X的平方根(二分法) 题目
分析
主要二分法找k的平方是不是小于x,然后二分法找
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public int mySqrt(int x) { int l = 0, r = x, ans = -1; //找不到就是-1 while (l <= r) { int mid = l + (r - l) / 2; //中间位置 if ((long)mid * mid <= x) { ans = mid; l = mid + 1; //在右边 } else { r = mid - 1; //在左边 } } return ans; } }
结果
矩阵置零(Set集合存对应行和列) 题目
分析 新建两个set集合存放是0的行和列,然后双重循环遍历是有对应的行和列就将原来数组置0.代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int m=input.nextInt(); int n=input.nextInt(); int[][] a=new int[m][n]; for(int i=0;i<m;i++){ for(int j=0;j<n;j++) { a[i][j] = input.nextInt(); } } setZeroes(a); //调用方法进行置0操作 for(int i=0;i<m;i++){ for(int j=0;j<n;j++) { System.out.print(a[i][j]+" "); } System.out.println(); } } public static void setZeroes(int[][] matrix) { int R = matrix.length; //获取行 int C = matrix[0].length; //获取列 Set<Integer> rows = new HashSet<Integer>(); //存取有0的行 Set<Integer> cols = new HashSet<Integer>(); //存取有0的列 //双重循环将是0的行和列存入到对应的set集合 for (int i = 0; i < R; i++) { for (int j = 0; j < C; j++) { if (matrix[i][j] == 0) { //存入对应的行和列 rows.add(i); cols.add(j); } } } //将对应的置0 for (int i = 0; i < R; i++) { for (int j = 0; j < C; j++) { if (rows.contains(i) || cols.contains(j)){ //set里面有 matrix[i][j] = 0; //数组里面的元素清0 } } } } }
结果
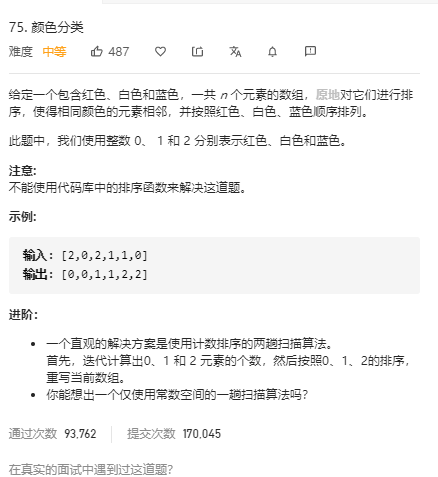
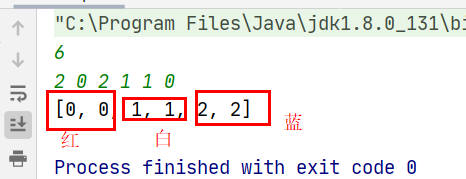
颜色分类(Sort/三个list集合) 题目
分析 1. 使用内置函数
2. 使用三个list集合分别存储对应旗的数字 然后按序输出代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++){ a[i] = input.nextInt(); } sortColors(a); System.out.println(Arrays.toString(a)); } public static void sortColors(int[] nums) { //1.使用内置函数 //Arrays.sort(nums); //2.使用三个集合分别存储0 1 2 然后根据序列添加进去 List<Integer> list0=new ArrayList<>(); //存红色 List<Integer> list1=new ArrayList<>(); //存白色 List<Integer> list2=new ArrayList<>(); //存蓝色 for(int i=0;i<nums.length;i++){ if(nums[i]==0){ list0.add(nums[i]); } if(nums[i]==1){ list1.add(nums[i]); //三个if就是将对应的数字存颜色内的list集合 } if(nums[i]==2){ list2.add(nums[i]); } } int lenyi=list0.size(); //获取三个长度 int lener=list1.size(); int lensan=list2.size(); for(int i=0;i<lenyi;i++){ nums[i]=list0.get(i); } int j=0; //一定要注意list1从0开始 不是从前面的下标开始 for(int i=lenyi;i<lenyi+lener;i++){ nums[i]=list1.get(j++); } int z=0; for(int i=lenyi+lener;i<lenyi+lener+lensan;i++){ nums[i]=list2.get(z++); } } }
结果
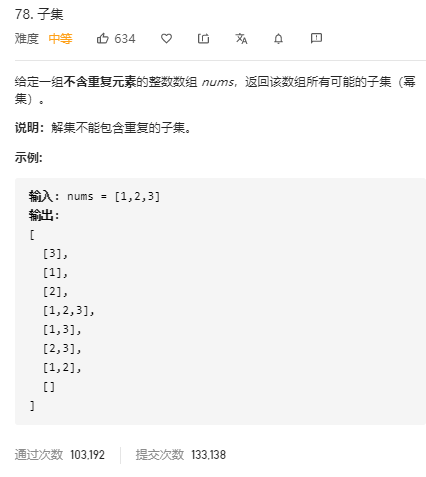
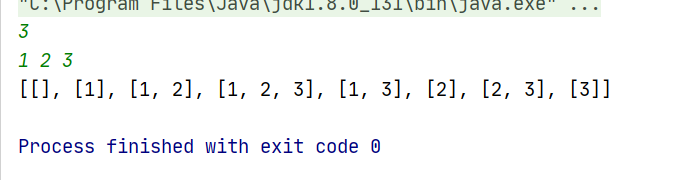
子集(回溯/递归) 题目
分析 1. 递归:可以通过递归不断的取元素放入list集合
2. 回溯:不断的循环每次去取子集,直到这一次取结束之后就返回代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++){ a[i] = input.nextInt(); } System.out.println(subsets(a)); } public static List<List<Integer>> subsets(int[] nums) { List<List<Integer>> res=new ArrayList<>(); //新建res集合接最终结果 backtrack(0, nums, res, new ArrayList<Integer>()); //调用方法 return res; //返回结果 } private static void backtrack(int i, int[] nums, List<List<Integer>> res, ArrayList<Integer> temp) { res.add(new ArrayList<>(temp)); //将temp添加到最终的res for(int j=i;j<nums.length;j++){ temp.add(nums[j]); //添加数组元素 backtrack(j+1,nums,res,temp); //进行下一次回溯i=j+1 temp.remove(temp.size()-1); //temp集合移除 } } }
结果
单词搜索(回溯/bfs/dfs) 题目
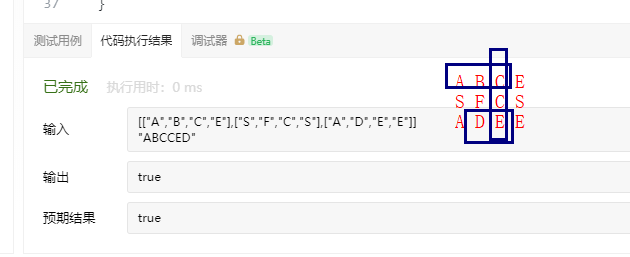
分析 1. 题目分析:他就是回溯方式让你去找能够匹配字符串的路径,不能重复使用同一个位置。
2. 回溯/dfs/bfs:
exist方法里面双重循环找第一个匹配的位置和调用回溯方法
backtrack方法里面就是变true然后再false进行回溯代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 public static boolean exist(char[][] board, String word) { int hang=board.length; //获取数组的行 int lie=board[0].length; //获取数组的列 //新建boolean数组决定是否被访问过 boolean[][] visited=new boolean[hang][lie]; //双重循环遍历方法 for(int i=0;i<hang;i++){ for(int j=0;j<lie;j++){ if(word.charAt(0)==board[i][j]&&backtrack(i,j,0,word,visited,board)){ return true; //找到第一个位置 然后调用方法 } } } return false; } private static boolean backtrack(int i, int j, int idx, String word, boolean[][] visited, char[][] board) { if(idx==word.length()){ return true; //如果下标到要查找的字符串的长度就说明ok } if(i>=board.length||i<0||j>=board[0].length||j<0||board[i][j]!=word.charAt(idx)||visited[i][j]){ return false; //不满足条件的情况都为false } visited[i][j]=true; //其他情况都为走过 if(backtrack(i + 1, j, idx + 1, word, visited, board) || //上下左右四个区域能找到就返回true backtrack(i - 1, j, idx + 1, word, visited, board) || backtrack(i, j + 1, idx + 1, word, visited, board) || backtrack(i, j - 1, idx + 1, word, visited, board) ){ return true; } visited[i][j]=false; //回溯 return false; } }
结果
分割回文串(回溯) 题目
分析 1. 使用双指针判断一部分代码是否是回文串(循环分为两部分)
2. 第一部分backtrack字符串剩下部分,第而部分进行判断回文串代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s=input.next(); //输入字符串 System.out.println(partition(s)); //调用方法获取结果 } public static List<List<String>> partition(String s) { List<List<String>> res = new ArrayList<>(); //res接受结果 backtrack(res, s, new ArrayList<String>()); //调用方法 return res; } private static void backtrack(List<List<String>> res, String s, ArrayList<String> tmp) { if (s == null || s.length() == 0) { res.add(new ArrayList<>(tmp)); //如果字符串不存在 就返回tmp新的list集合 [] } for (int i = 1; i <= s.length(); i++) { if (isPalidrome(s.substring(0, i))) { //如果截取的这部分是回文串 tmp.add(s.substring(0, i)); //tmp集合存放s的部分 backtrack(res, s.substring(i, s.length()), tmp); //找i之后的部分 前面的s被tmp集合用了 tmp.remove(tmp.size() - 1); //回溯 } } } private static boolean isPalidrome(String sb) { int left = 0; //左指针 int right = sb.length() - 1; //右指针 while (left < right) { //左右不碰面 if (sb.charAt(left) != sb.charAt(right)) { return false; //如果左右不相等 就返回false } left++; //向中间靠拢 right--; } return true; } }
结果
只出现一次的数(异或) 题目
分析 1. 异或中任何数和0异或都是自己,自己和自己异或就是0
2. 因为题目中只有一个数出现一次,其他都是两次,所以所有数字异或的话出现两次的最后异或是0然后0和出现一次的数字异或就是出现一次的结果 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++){ a[i] = input.nextInt(); } System.out.println(singleNumber(a)); } public static int singleNumber(int[] nums) { int single = 0; for (int num : nums) { single ^= num; //所有数字异或的结果就是出现了一次的数字 } return single; } }
结果
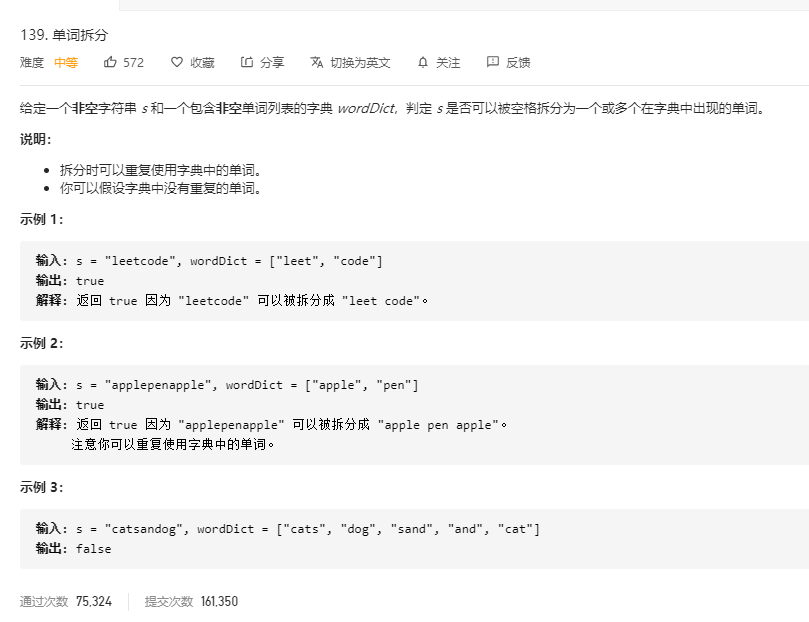
单词拆分(动态规划) 题目
分析
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s=input.next(); int n=input.nextInt(); List<String> list=new ArrayList<>(); for(int i=0;i<n;i++){ list.add(input.next()); } System.out.println(wordBreak(s,list)); } public static boolean wordBreak(String s, List<String> wordDict) { int n=s.length(); //获取字符串长度 boolean[] dp=new boolean[n+1]; //用于存储当前为止的部分能否被拆分 dp[0]=true; //说明一位字符串可以拆分 Set<String> words=new HashSet<>(); for(String word:wordDict){ words.add(word); //将list集合都存入到words的set集合 } for(int i=1;i<=n;i++){ for(int j=0;j<i;j++){ if(dp[j]&&words.contains(s.substring(j,i))){ dp[i]=true; //dp[j]中j之前的可以拆分 而且j-i在list集合内 } } } return dp[n]; //返回最后一个值 就是字符串这么长的能否拆分 } }
结果
乘积最大子数组(动态规划) 题目
分析 我们只要记录前i的最小值和最大值
满足:dp[i] = max(nums[i] * pre_max, nums[i] * pre_min, nums[i])代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++){ a[i]=input.nextInt(); } System.out.println(maxProduct(a)); } public static int maxProduct(int[] nums) { if (nums == null || nums.length == 0) { //如果数组不存在或者长度为0 return 0; //返回乘积0 } int res = nums[0]; //接最后结果 int pre_max = nums[0]; int pre_min = nums[0]; for (int i = 1; i < nums.length; i++) { //从下标1的位置开始 //每一次获取当前循环的min和max int cur_max = Math.max(Math.max(pre_max * nums[i], pre_min * nums[i]), nums[i]); int cur_min = Math.min(Math.min(pre_max * nums[i], pre_min * nums[i]), nums[i]); res = Math.max(res, cur_max); //不断替换 pre_max = cur_max; pre_min = cur_min; } return res; } }
结果
寻找峰值(分类讨论) 题目
分析 1. 一直递增: 最后一个位置就是输出的下标
2. 一直递减: nums[i] > nums[i + 1] (第一个位置)
3. 中间有最高的: nums[i] > nums[i + 1] (顶峰)代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++){ a[i]=input.nextInt(); } System.out.println(findPeakElement(a)); } public static int findPeakElement(int[] nums) { for (int i = 0; i < nums.length - 1; i++) { //大的一侧一定是峰值!!!!!!!!!!! if (nums[i] > nums[i + 1]) { return i; // 3 > 2 -- 输出3的下标 } } return nums.length - 1; //一直增高 所以最高的是最后一个位置 } }
结果
多数元素(一半以上) 题目
分析 1. 使用Arrays.sort()排序之后出现一半以上的数字肯定是排序之后的中间数字。
2. 使用哈希表(hashmap)存储然后返回值最大的键。代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++){ a[i]=input.nextInt(); } System.out.println(majorityElement(a)); } public static int majorityElement(int[] nums) { if(nums.length==0){ return 0; } Arrays.sort(nums); return nums[nums.length/2]; } }
结果
Excel表列序号(26进制) 题目
分析 1. 字符串转字符数组这样方便后面的按位计算结果。
2. 倒序从最后一位开始乘积,使用j记录每次是要乘16的几次方,然后res得到结果。代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s=input.next(); System.out.println(titleToNumber(s)); } public static int titleToNumber(String s) { char[] a=s.toCharArray(); //字符串转字符数组 int res=0; //获取结果 int j=0; for(int i=a.length-1;i>=0;i--){ //倒序乘积 res+=(int)(a[i]-64)*Math.pow(26,j); j++; //每一次都会是16的倍数 } return res; } }
结果
快乐数(10进制) 题目
分析 1. 使用while循环添加n进入set结合,然后不断更新n
2. 更新n:就是通过拆分十进制然后进行平方计算代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); System.out.println(isHappy(n)); } public static boolean isHappy(int n) { Set<Integer> set=new HashSet<>(); while(n!=1&&!set.contains(n)) { //没出现 set.add(n); //set集合里面添加n n = getNext(n); //调用方法得到新的n } return n == 1; //判断结果是不是1 } private static int getNext(int n) { int totalSum = 0; while (n > 0) { int d = n % 10; //拆分 n = n / 10; totalSum += d * d; //得到n这个数字每一位最终的结果 } return totalSum; } }
结果
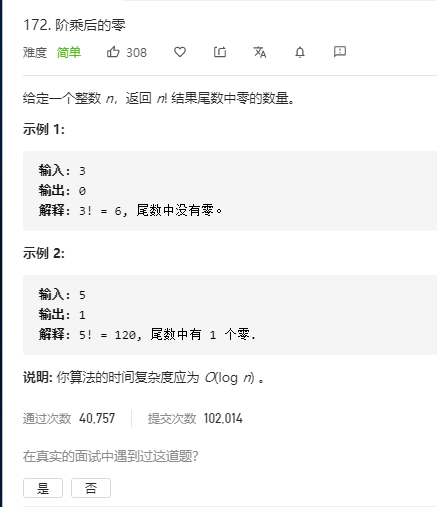
阶乘后的零(递归+拆分/5的个数) 题目
分析
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 //第一种:先递归算答案+拆分得到结果 public class Jump { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); long res=trailingZeroes(n); //获阶乘的结果 int ge=jige(res); System.out.println(ge); } public static long trailingZeroes(int n) { long res=0; if(n==0||n==1){ res=1; //0!=1 } if(n==2){ res=2; //2!=2*1=2 }else{ res=trailingZeroes(n-1)*n; } return res; } private static int jige(long res) { int ge=0; //0的个数 long j=0; while(res!=0){ j=res%10; if(j==0){ ge++; } if(j!=0){ break; } res=res/10; } return ge; } } //第二种:得到5的个数 public static int trailingZeroes(int n) { int count = 0; //获取的结果 //一个5提供一个0,一个25提供2个0; while (n > 0) { //n大于0就行 count+=n/5; n=n/5; } return count; }
结果
最大数(排序) 题目
分析 1. 重写compare方法,就是用于比较
2. 通过将数组转字符串数组,然后进行排序之后再贴合上去就行代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution { private class LargerNumberComparator implements Comparator<String> { @Override public int compare(String a, String b) { String o1 = a + b; String o2 = b + a; return o2.compareTo(o1); } } public String largestNumber(int[] nums) { String[] s = new String[nums.length]; for (int i = 0; i < nums.length; i++) { s[i] = String.valueOf(nums[i]); //将对应的数字传到s的字符串数组 } Arrays.sort(s, new LargerNumberComparator()); //排序 if (s[0].equals("0")) { return "0"; //如果有0就返回0 } String res = new String(); for (String numAsStr : s) { res+= numAsStr; //循环将s数组贴合在字符串res上 } return res; } }
结果
旋转数组(新建数组放) 题目
分析 1. 新建数组b
2. 通过下标的倾斜存入新的数组b
3. 主函数调用输出代码 1 2 3 4 5 6 7 8 9 public void rotate(int[] nums, int k) { int[] a = new int[nums.length]; for (int i = 0; i < nums.length; i++) { a[(i + k) % nums.length] = nums[i]; } for (int i = 0; i < nums.length; i++) { nums[i] = a[i]; } }
结果
颠倒二进制位(位运算) 题目
分析 主要基于位运算!!! 代码 1 2 3 4 5 6 7 8 9 10 11 12 public int reverseBits(int n) { int res = 0; int count = 0; while (count < 32) { res <<= 1; //res 左移一位空出位置 res |= (n & 1); //得到的最低位加过来 n >>= 1;//原数字右移一位去掉已经处理过的最低位 count++; } return res; }
结果
位1的个数/汉明重量(Integer.bitCount()方法/位运算) 题目
分析 1. 直接使用Integer.bitCount(n)方法:获取二进制中1的个数
2. 使用位运算n=n&(n-1)将最右边的末位数字的1变为0,直到n为0就结束代码 1 2 3 4 5 6 7 8 9 public static int hammingWeight(int n) { int flag=0; //记录最终1的个数 while(n!=0){ //直到n最后所有1都变成0 整体为0就结束 flag++; //1的个数加1 n=n&(n-1); //不断的取最右边的一位1变为0 } System.out.println(flag); //位运算输出 return Integer.bitCount(n); //第一种方法 }
结果
计数质数(暴力法/筛法) 题目
分析 1. 质数概念: 除了自己和1以外找不到另外一个数字可以整除
2. 暴力循环: 双层for循环判断,然后累加计数器(需要把边界值考虑掉)
3. 埃拉托斯特尼筛法:其实就是找到质数,然后它的所有倍数肯定也不是,这样不用一个一个判断。
(例如:当前判断2,则4,6,8等等一直到n的数字都不是质数)代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 //1.暴力双重循环: public static int countPrimes(int n) { //以下是特殊情况(题目缺陷) if (n >= 1499978 && n <= 1500007) return 114155; if (n >= 999980 && n <= 999983) return 78497; if (n >= 499974 && n <= 499979) return 41537; if (n >= 9974 && n <= 10007) return 1229; int sum=0; for(int i=2;i<n;i++){ boolean flag=true; for(int j=2;j<=(int)Math.sqrt(i);j++){ if(i%j==0){ flag=false; break; } } if(flag){ sum++; } } return sum; } //2.筛法: public int countPrimes(int n) { // 1. 给0 - n之间的数加上标记 byte[] nums = new byte[n]; for (int i = 0; i < n; i++) { nums[i] = 1; } // 2. 对于非质数,进行标记清除 for (int i = 2; i < n; i++) { // 如果当前数为质数 if (nums[i] == 1) { // 将当前数作为基数,筛掉其倍数的数字 for (int j = 2; i * j < n; j++) { // 标记清除 nums[i*j] = 0; //i的倍数都清除 } } } //3. 遍历数组,统计质数(元素值==1) int count = 0; for (int i = 2; i < n; i++) { if (nums[i] == 1) count++; } return count; }
结果
数组中的第K个最大元素(sort()/快排) 题目
分析 1.Arrays.sort(数组名)
2.快排等各种排序代码 1 2 3 4 5 6 //1.使用Java自带sort排序方法 public static int findKthLargest(int[] nums, int k) { Arrays.sort(nums); return nums[nums.length-k]; }
结果
存在重复元素(排序遍历/set集合) 题目
分析 1. 使用set集合contains方法判断是否出现第二次(true)
2. 先对数组排序,之后判断前后是否有相等的数据代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 //1.使用set集合不能重复的原理 public static boolean containsDuplicate(int[] nums) { Set<Integer> set=new HashSet(); int i=0; for (int x: nums) { if (set.contains(x)) return true; set.add(x); } return false; } //2.先排序之后,通过遍历查看前后是否有相等的情况 public boolean containsDuplicate(int[] nums) { Arrays.sort(nums); for (int i = 0; i < nums.length - 1; ++i) { if (nums[i] == nums[i + 1]) return true; } return false; }
结果
基本计算器(分情况叠加) 题目
分析 思路:
1. 字符串转字符数组,
2. 循环将数字叠加起来然后通过判断语句,
3. 进行四则运算,然后每次结果放入一个stack数组内,不断的取出更换
4. 最后循环遍历将数组所有值叠加起来输出即可 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 class Solution { public int calculate(String s) { //字符串长度 int len = s.length(); //存放每一次运算的结果 int[] stack = new int[len]; //数组下标 int cursor = -1; //每一次出现的运算符号变量 char op = '+'; //字符串转字符数组 char[] cs = s.toCharArray(); for (int i=0; i<len; i++) { //获取每一位字符串的当前位置 char c = cs[i]; //空格继续进行跳过这次循环 if (c == ' ') continue; //如果是数字 if (Character.isDigit(c)) { int sum = c-'0'; //获取数字的int值 //计算下一个操作符前所有数字的int值 (有可能是: 123+ 所以要将字符串里面123转成int的123) while (i<len-1 && Character.isDigit(cs[i+1])) { sum = sum*10 + (cs[++i]-'0'); } //判断四则运算然后计算结果 switch (op){ case '+' -> stack[++cursor] = sum; case '-' -> stack[++cursor] = -sum; case '*' -> stack[cursor] *= sum; case '/' -> stack[cursor] /= sum; } } else op = c; } //循环遍历得到结果 int ans = 0; for (int num : stack) { ans += num; } return ans; } }
结果
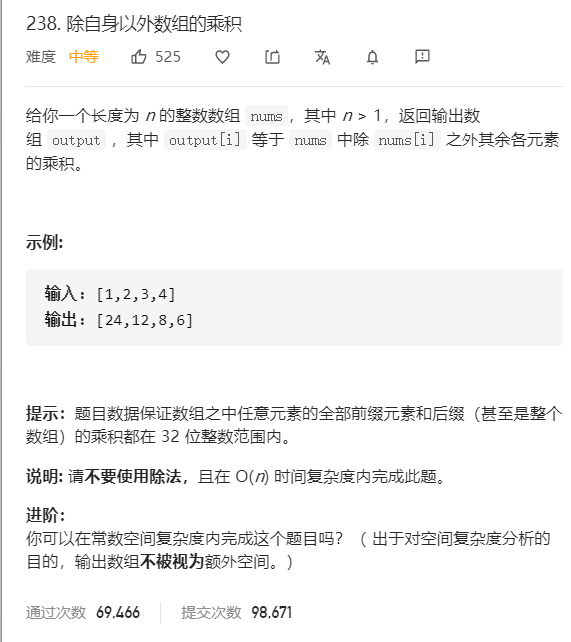
除自身以外数组的乘积(讨论0的个数) 题目
分析 1. 其实就是统计0的个数:
1.1 0的个数大于2: 所有位置的值都是0
1.2 0的个数等于1: 0位置的值是总乘积sum 其他位就是0
1.3 0的个数为0(最不特殊的情况): 总乘积sum/当前位置值
2. 举例:
2.1 输入0 0 2 3 1 不管哪个位置计算的时候总有一个0存在 所以都是0
2.2 输入0 1 2 5 8 只有0的位置的值是其他乘积 其他位置都会有一个0所以是0
2.3 输入1 3 2 5 9 所有位置都不为0 所以是最广泛普通的总成绩sum/当前值代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++) { a[i] = input.nextInt(); } System.out.println(Arrays.toString(productExceptSelf(a))); } //考虑最大的范围就是所有乘积max 然后每位除当前值就是答案 public static int[] productExceptSelf(int[] nums) { int len=nums.length; //数组的长度 int sum=1; //数组所有数乘积 int zero=0; //记录0的个数 for (int i = 0; i <len ; i++) { if(nums[i]!=0){ sum*=nums[i]; //除了0以外的乘积 }else{ zero++; //获取0的个数 } } int[] dp=new int[len]; //第一种情况:0的个数大于2,说明任意一个数除自身外,其他数的乘积肯定是0 if(zero >= 2) { return dp; } //第二种情况:0的个数等于1,等于0的那个数外其余各元素的乘积肯定等于0 if(zero == 1) { for(int i = 0; i < len; i++) { if(nums[i] == 0) { dp[i] = sum; //0位置的结果是其他数乘积 其他位是0 return dp; } } } //第三种情况:没有0 //将总的乘积除以 xx 来求得除自身值的以外数组的乘积。 else{ for(int i = 0; i < len; i++) { dp[i] = sum / nums[i]; //最不特殊的情况就是每位都是sum/当前值 } } return dp; } }
结果
搜索二维矩阵(双指针) 题目
分析 1. 暴力法:二层循环找到就true找不到false
2. 双指针法:
2.1 找到就true
2.2 双指针位置<target 说明左边的也小 我们要换下一行
2.3 双指针位置>target 说明上面的也大 我们要换前面列代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); int[][] a=new int[][]{{1, 4, 7, 11, 15}, {2, 5, 8, 12, 19}, {3, 6, 9, 16, 22}, {10, 13, 14, 17, 24}, {18, 21, 23, 26, 30}}; int target=input.nextInt(); System.out.println(searchMatrix(a,target)); } public static boolean searchMatrix(int[][] matrix, int target) { int hang=matrix.length; //二维数组行 int lie=matrix[0].length; //二维数组列 int h=0; //指向行的指针 int l=lie-1; //指向列的指针 while(h<hang&&l>=0){ if(matrix[h][l]>target){ l--; //列向左 }else if(matrix[h][l]<target){ h++; //行向下 }else{ return true; //找到目标元素 } } return false; } }
结果
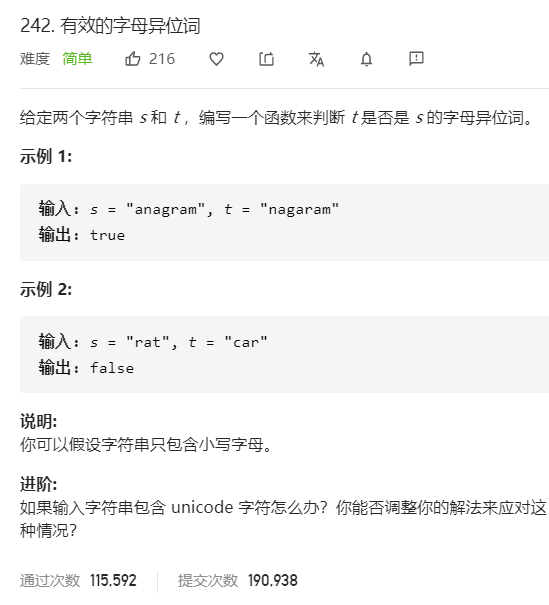
有效的字母异位词(排序/哈希表) 题目
分析 1. 排序: 字符串转字符数组然后排序,使用equals方法对比即可
2. 哈希表(计数器):设计一个26位计数器,通过记录s的单词频率,然后用t的去减掉,如果计数器到了0就说明ok代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 //1.排序之后查看是否相同 public boolean isAnagram(String s, String t) { if (s.length() != t.length()) { return false; //长度不同就false } char[] str1 = s.toCharArray(); char[] str2 = t.toCharArray(); Arrays.sort(str1); //对两个字符串字符数组排序 Arrays.sort(str2); return Arrays.equals(str1, str2); //返回是否相同 } //2.计数器 public boolean isAnagram(String s, String t) { if (s.length() != t.length()) { return false; //长度不同就false } int[] counter = new int[26]; //26位的计数器 for (int i = 0; i < s.length(); i++) { counter[s.charAt(i) - 'a']++; //s存进去 counter[t.charAt(i) - 'a']--; //t取出来 } for (int count : counter) { if (count != 0) { return false; //如果有计数器不回归到0就false } } return true; }
结果
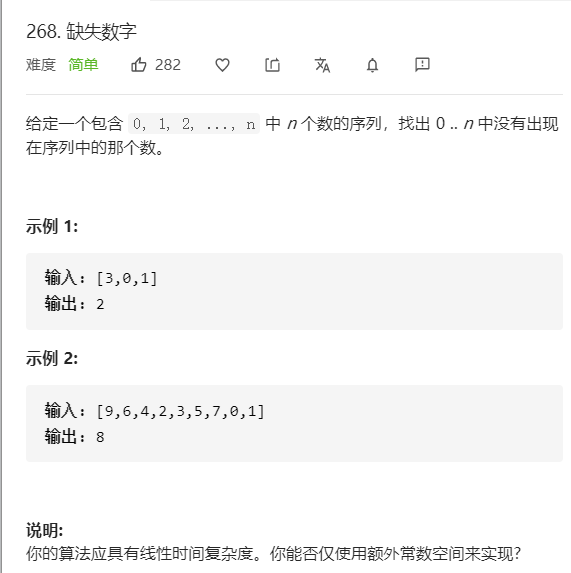
缺失数字(异或/等差数列/双指针/数学法) 题目
分析 1. 双指针:不断缩小范围看是在左边还是右边的区域
2. 异或:(类似于找只出现过一次的值)
2.1 所有数组元素异或
2.2 0-n的数字异或
2.3 就相当于出现过的数字是异或两次(自己异或自己是0),然后没出现的数字两次异或只会出现一次(0和没出现的数字异或是没出现的数字)代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for(int i=0;i<n;i++) { a[i] = input.nextInt(); } System.out.println(missingNumber(a)); } public static int missingNumber(int[] nums) { int que=0; //1. 数组内元素异或 for(int i=0;i<nums.length;i++){ que^=nums[i]; } //2. 0-n异或 for(int i=0;i<nums.length+1;i++){ que^=i; } return que; } }
结果
完全平方数(回溯/动态规划) 题目
分析 思路:先把n减去一个平方数,然后求剩下的数分解成平方数和所需的最小个数
假设输入的n = 12
1.把 n 减去 1, 然后求出 11 分解成平方数和所需的最小个数,记做 n1,那么当前方案总共需要 n1 + 1 个平方数
2.把 n 减去 4, 然后求出 8 分解成平方数和所需的最小个数,记做 n2,那么当前方案总共需要 n2 + 1 个平方数
3.把 n 减去 9, 然后求出 3 分解成平方数和所需的最小个数,记做 n3,那么当前方案总共需要 n3 + 1 个平方数
4.下一个平方数是16,结束
5.然后对比选出最小情况值代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 //第一种:未优化版本(重复答案会超时) public static int numSquares(int n) { return numSquaresHelper(n); //调用方法 } private static int numSquaresHelper(int n) { if(n==0){ return 0; } int count=Integer.MAX_VALUE; for(int i=1;i*i<=n;i++){ count=Math.min(count,numSquaresHelper(n-i*i))+1; //不断的取方案求最小值 } return count; } //第二种:利用map集合存储(减少重复使用,提高效率) public static int numSquares(int n) { return numSquaresHelper(n,new HashMap<Integer,Integer>()); //使用map集合 } private static int numSquaresHelper(int n,HashMap<Integer,Integer> map) { if (map.containsKey(n)) { //输入的元素在map内 return map.get(n); //返回这个数字时候的最小值 } if(n==0){ return 0; //找0的就返回0 } int count=Integer.MAX_VALUE; for(int i=1;i*i<=n;i++){ count=Math.min(count,numSquaresHelper(n-i*i,map)+1); //其实就是之前的优化结果集 } map.put(n,count); //将每个n对应的答案都存起来(好取不然会时间爆了) return count; }
结果
移动零(简单赋值) 题目
分析 1. 先把非0的补进去,补完了后面补0代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for (int i = 0; i <n ; i++) { a[i]=input.nextInt(); } moveZeroes(a); System.out.println(Arrays.toString(a)); } public static void moveZeroes(int[] nums) { if(nums==null) { return; //数组不存在 } //第一次遍历的时候,j指针记录非0的个数,只要是非0的统统都赋给nums[j] int j = 0; for(int i=0;i<nums.length;++i) { if(nums[i]!=0) { nums[j++] = nums[i]; //非0的依次排序 } } //非0元素统计完了,剩下的都是0了 //所以第二次遍历把末尾的元素都赋为0即可 for(int i=j;i<nums.length;++i) { nums[i] = 0; //从后面开始补0 } } }
结果
寻找重复值(遍历/二分法) 题目
分析 1. 遍历:先排序之后我们可以依次遍历查看前后是否有重复的,重复就输出即可
2. 二分法:就是分为两段查看两段的差和数组差大小,不断挪动指针最后得到结果
2.1 举例: 1 2 3 4 5 5 6
我们第一就可以判断1 2 3没有重复 中间差和数组差一样
判断5 5 6有重复 因为本来应该是到7但是有重复只到了6代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 //1.排序之后如果前后一样就重复输出 public static int findDuplicate(int[] nums) { int res=0; Arrays.sort(nums); for (int i = 0; i < nums.length-1; i++) { if(nums[i]==nums[i+1]){ return nums[i]; } } return res; } //2.二分法 public static int findDuplicate(int[] nums) { int n = nums.length; int l = 1, r = n - 1, ans = -1; while (l <= r) { //左<=右 int mid = (l + r) >> 1; //中间位置 int cnt = 0; for (int i = 0; i < n; ++i) { if (nums[i] <= mid) { cnt++; } } if (cnt <= mid) { l = mid + 1; //重复的在右边 } else { r = mid - 1; //重复的在左边 ans = mid; } } return ans; }
结果
最长上升子序列(动态规划) 题目
分析
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for (int i = 0; i <n ; i++) { a[i]=input.nextInt(); } System.out.println(lengthOfLIS(a)); } public static int lengthOfLIS(int[] nums) { if (nums.length == 0) { return 0; //数组长度为0 } int[] dp = new int[nums.length]; Arrays.fill(dp, 1); //数组都补充1 int res = 0; for (int i = 0; i < nums.length; i++) { for(int j=0;j<i;j++){ if(nums[j] < nums[i]){ //说明可以贴在后面 dp[i] = Math.max(dp[i], dp[j] + 1); } } res = Math.max(res, dp[i]); } return res; } }
结果
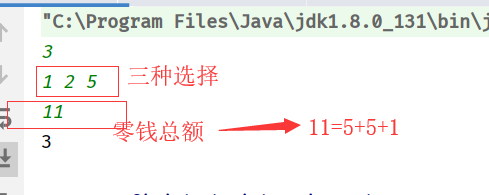
零钱兑换(回溯/动态规划) 题目
分析 其实跟之前的找平方数题一样,这种题目使用回溯和动态规划!代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for (int i = 0; i <n ; i++) { a[i]=input.nextInt(); } int amount=input.nextInt(); System.out.println(coinChange(a,amount)); } public static int coinChange(int[] coins, int amount) { //零钱相当于物品,总金额相当于背包容量 int [] dp=new int[amount+1];//dp[i][j]:对前i个零钱,选若干兑换总金额为j的整钱,最少需要的零钱个数为dp[i][j] dp[0]=0;//0个零钱,待兑换总金额为0,最少0个零钱就能满足 for(int i=1;i<=amount;i++){ dp[i]=amount + 1; // amount + 1 是不可能达到的换取数量,于是使用其进行填充 } //dp的过程是取Min //一维数组dp[j]里的j指的是背包容量,这里即总金额 for(int i=1;i<=coins.length;i++){//对前i个零钱,其中第i个零钱是coins[i-1] for(int j=coins[i-1];j<=amount;j++){//完全背包正序更新一维数组 dp[j]=Math.min(dp[j],dp[j-coins[i-1]]+1);//根据背包九讲:求最小价值/最少件数,只需将原始状态转移方程中的max改成min } } return dp[amount]==amount + 1?-1:dp[amount]; } }
结果
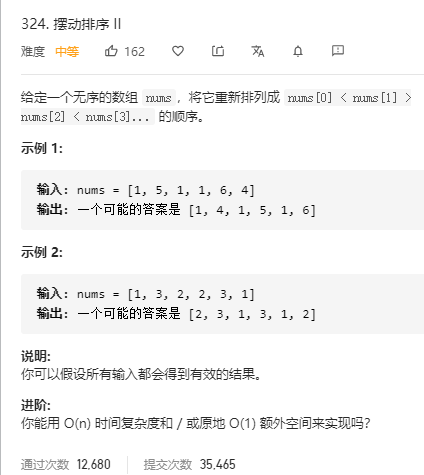
摆动排序(分类) 题目
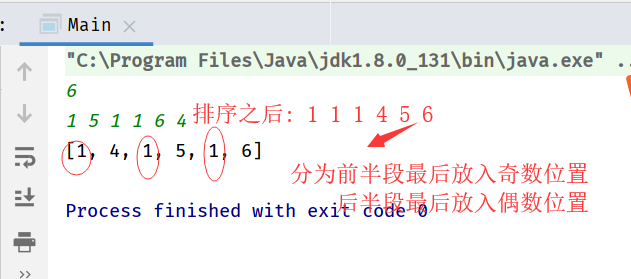
分析 其实就是排序之后将前半段倒序放入奇数位置,后半段倒序放入偶数位置。
举例:输入 1 3 2 2 3 1
排序之后1 1 2 2 3 3(分为1 1 2和2 3 3)
倒序输入前半段: 2 X 1 X 1 X
倒序输入后半段: 2 3 1 3 1 2代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 /** * 先排序再穿插 * O(nlogn)+O(n)=O(nlogn) */ public void wiggleSort(int[] nums) { //排序 Arrays.sort(nums); int len=nums.length,i = 0; int[] smaller=new int[len%2==0?len/2:(len/2+1)],bigger=new int[len/2]; //复制 System.arraycopy(nums,0,smaller,0,smaller.length); System.arraycopy(nums,smaller.length,bigger,0,len/2); //穿插 for (; i < len / 2; i++) { nums[2*i]=smaller[smaller.length-1-i]; nums[2*i+1]=bigger[len/2-1-i]; } if (len%2!=0) nums[2*i]=smaller[smaller.length-1-i]; } }
结果
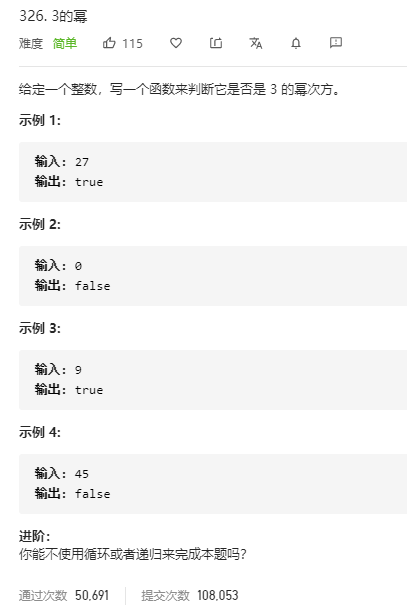
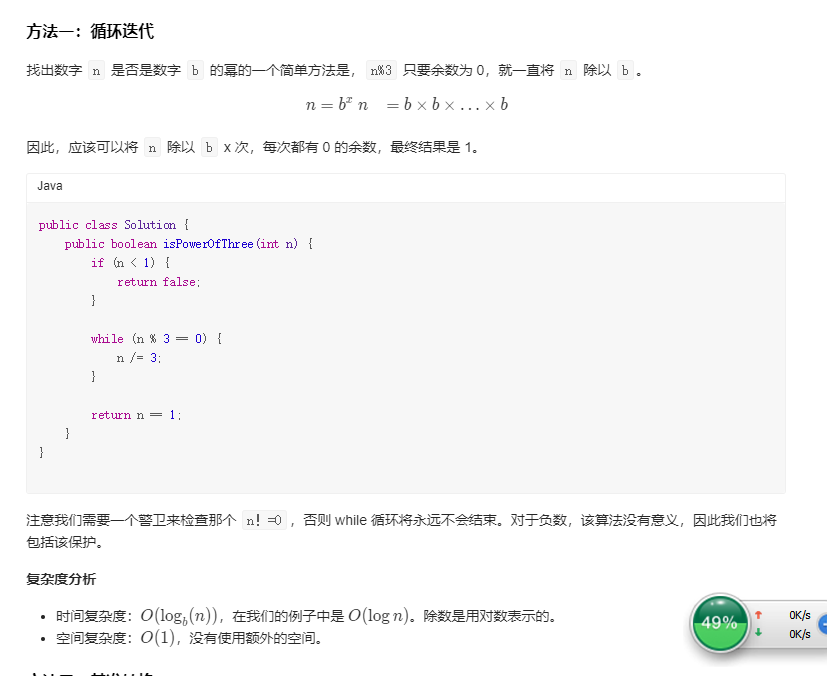
3的幂(循环迭代) 题目
分析
代码 1 2 3 4 5 6 7 8 9 10 11 public boolean isPowerOfThree(int n) { if (n < 1) { return false; //如果是0肯定返回0 } while (n % 3 == 0) { n /= 3; //n不断除3 } return n == 1; //最后看是不是等于1 }
结果
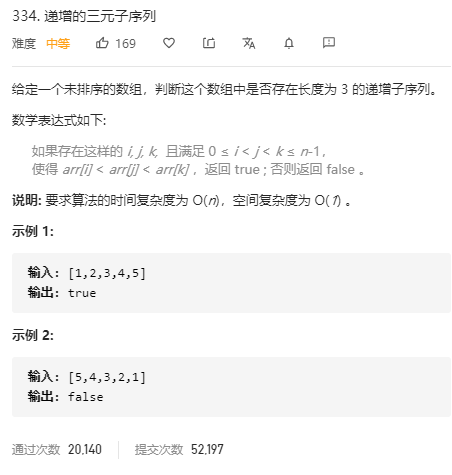
递增的三元子序列(类似于动态规划) 题目
分析 结合最长上升子序列那道题的二分贪心解法:
1. 我只需要维护2个变量,分别保存3元上升子序列的第一个值firstMin和第二个值secondMin
2. 当nums[i]<firstMin : 更新firstMin
3. 当firstMin<nums[i]<secondMin : 更新secondMin
4. 这样就能够保证前两个尽可能地小,也就是最有可能找到三元上升子序列 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for (int i = 0; i <n ; i++) { a[i]=input.nextInt(); } System.out.println(increasingTriplet(a)); } public static boolean increasingTriplet(int[] nums) { int len=nums.length; //获取数组长度 if(nums.length<3){ return false; //长度<3 不会找到长度为3的子序列 } int firstMin = Integer.MAX_VALUE; //第一小 int secondMin = Integer.MAX_VALUE; //第二小 for(int i=0;i<nums.length;i++) { if(nums[i]>secondMin){ return true; //能找到第三个数字 } if(nums[i]<=firstMin){ firstMin=nums[i]; //找到第一小 } else if(nums[i]<secondMin){ // firstMin<nums[i]<secondMin secondMin=nums[i]; //找到第二小 } } return false; //默认找不到 } }
结果
反转字符串(双指针) 题目
分析 1. 不增额外的空间,使用双指针不断挪里面挪动,使用temp中间值交换两边的值。代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s1=input.next(); //输入一个字符串 char[] s=s1.toCharArray(); //字符串转字符数组 reverseString(s); //反转 System.out.println(Arrays.toString(s)); //字符数组输出 } public static void reverseString(char[] s) { // 左右双指针 int left = 0; int right = s.length - 1; // 交换元素的临时变量 temp char temp; while (left < right){ temp = s[left]; s[left++] = s[right]; //不断往里面缩小 s[right--] = temp; } } }
结果
前k个高频元素(栈+HashMap集合) 题目
分析 1. 新建map集合存放对应值和出现次数;maxheap根据map集合存放所有<Key,Value>;result数组存放最后弹出来的k个key值
2. 先for遍历存放进去所有的key和value对
3. 然后通过(a,b) -> b.getValue() - a.getValue()对于键值对会有排序
4. 然后通过栈先进后出的原理,相当于倒序输出最大的k个key值代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); int n=input.nextInt(); int[] a=new int[n]; for (int i = 0; i <n ; i++) { a[i]=input.nextInt(); } int k=input.nextInt(); System.out.println(Arrays.toString(topKFrequent(a,k))); } public static int[] topKFrequent(int[] nums, int k) { //存放key-value这样的形式 存放每个元素出现次数 Map<Integer,Integer> map=new HashMap<>(); //进行排序 PriorityQueue<Map.Entry<Integer, Integer>> maxheap = new PriorityQueue<>((a,b) -> b.getValue() - a.getValue()); //存放结果的数组 int[] result = new int[k]; for (int i = 0; i < nums.length; i++) { map.put(nums[i],map.getOrDefault(nums[i],0)+1); //遍历存放每个key对应的value } for(Map.Entry<Integer, Integer> m : map.entrySet()){ maxheap.offer(m); //按照键值对放入maxhead中 } //倒序输出k个值就是结果 for(int i = 0; i < k; i++){ result[i] = maxheap.poll().getKey(); } return result; } }
结果
两个数组的交集II(哈希表hashmap/排序) 题目
分析 1. 使用map存,然后对应数组减少,然后相同的存到数组里面输出。代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public int[] intersect(int[] nums1, int[] nums2) { if (nums1.length > nums2.length) { return intersect(nums2, nums1); //反转数组 } Map<Integer, Integer> map = new HashMap<Integer, Integer>(); //map集合 for (int num : nums1) { int count = map.getOrDefault(num, 0) + 1; map.put(num, count); //遍历存放对应键值对 } int[] intersection = new int[nums1.length]; int index = 0; for (int num : nums2) { int count = map.getOrDefault(num, 0); if (count > 0) { intersection[index++] = num; count--; //有的话减少一个value值 if (count > 0) { map.put(num, count); } else { map.remove(num); } } } return Arrays.copyOfRange(intersection, 0, index); }
结果
两数求和(位运算) 题目
分析 1. 能使用加减乘除操作: return a+b;
2. 不使用加减乘除操作: 位运算
2.1 a^b得到不进位的值
2.2 (a&b)<<1得到进位值
2.3 不断进行前两步直到第二步的值为0结束代码 1 2 3 4 5 6 7 8 9 public int getSum(int a, int b) { while(b != 0){ int temp = a ^ b; b = (a & b) << 1; a = temp; } return a; }
结果
有序矩阵中第K小的元素(直接排序/归并排序/二分法) 题目
分析 1. 直接排序:使用一维数组a存放二维数组元素,然后排序之后输出a[k-1]就是结果代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); int[][] a=new int[][]{{1,5,9},{10,11,13},{12,13,15}}; int m=input.nextInt(); System.out.println(kthSmallest(a,m)); } public static int kthSmallest(int[][] matrix, int k) { int res=0; int len=matrix.length; //数组的行和列 int[] a=new int[len*len]; int z=0; for(int i=0;i<len;i++){ for(int j=0;j<len;j++){ a[z++]=matrix[i][j]; } } Arrays.sort(a); //进行排序 return a[k-1]; //返回第8个 } }
结果
字符串中第一个唯一字符(哈希表) 题目
分析 1. 使用hashmap集合存储键值对(每个字符和出现次数)
2. 遍历查询是否出现一次就返回(第一次出现)代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); String s=input.next(); System.out.println(firstUniqChar(s)); } public static int firstUniqChar(String s) { //存放字符出现次数和对应字符(键值对) HashMap<Character, Integer> count = new HashMap<Character, Integer>(); //字符串长度 int n = s.length(); //遍历存入map集合 for (int i = 0; i < n; i++) { char c = s.charAt(i); count.put(c, count.getOrDefault(c, 0) + 1); } //遍历找谁出现次数是1次 for (int i = 0; i < n; i++) { if (count.get(s.charAt(i)) == 1) return i; } return -1; //找不到返回-1 } }
结果
四数相加(哈希表) 题目
分析 1. 使用一个map集合存放a和b的和
2. 使用另外一个map集合存放c和d和的相反数
3. 最后判断是否相等,就说明相反相加是0代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public int fourSumCount(int[] A, int[] B, int[] C, int[] D) { Map<Integer, Integer> map = new HashMap<>(); //Map<Integer, Integer> map = new HashMap<>(); int res = 0; for(int i = 0;i<A.length;i++){ for(int j= 0;j<B.length;j++){ int sumAB = A[i]+B[j]; if(map.containsKey(sumAB)) map.put(sumAB,map.get(sumAB)+1); else map.put(sumAB,1); } } for(int i = 0;i<C.length;i++){ for(int j = 0;j<D.length;j++){ int sumCD = -(C[i]+D[j]); if(map.containsKey(sumCD)) res += map.get(sumCD); //增加有这个配对的key的value值 } } return res; }
结果