剑指offer

数组

二维数组的查找

面试三题目

题目分析

1. 使用暴力二重循环遍历
2. 使用题目中横竖都递增的原理：
    2.1 如果相等输出true
    2.2 目标n>a[i][j] 说明我们要找的比现在位置的要大 (这一行都比目标的小)所以下移一行 i++
    2.3 目标n<a[i][j] 说明我们要找的比现在位置的要小 (这一列都比目标的大)所以左移一列 j--

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class erweishuzuchazhao {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
          System.out.println("输入要查找的元素的值：");
2020/5/18 10:14:36           System.out.println("输入二维数组的行：");
            int h=input.nextInt();  //输入二维数组的行
          System.out.println("输入二维数组的列：");
            int l=input.nextInt();  //输入二维数组的列
            int[][] a =new int[h][l];
          System.out.println("输入二维数组内容：");
            //输入二维数组的值
                for(int i=0;i<h;i++){
                   for(int j=0;j<l;j++){
                    a[i][j]=input.nextInt();
                   }
                }
            //调用函数得到结果
               if(chazhao(a,n)==1){
                   System.out.println("要查询的"+n+"存在");
               }else{
                   System.out.println("要查询的值不存在");
               }
    }

  //1. 二维数组循环遍历(不推荐)
    public static int chazhao(int[][] a,int n){
        int f=0;
        for(int i=0;i<a.length;i++){
            for(int j=0;j<a[i].length;j++){
                if(a[i][j]==n)
                {
                    f=1;  //存在就赋值为11
                }
            }
        }
        return f;
    }

 //2. 布尔值判断
 public boolean Find(int n, int [][] a) {
        //判断数组空
        if((a==null||a.length==0)||(a.length==1&&a[0].length==0)){
            return false;
        }
        int i=0; //左上角
        int j=a[0].length-1;  //右上角
        while(i<=a[0].length-1&&j>=0){
            if(n==a[i][j]) {return true;}   //找到了
            if(n<a[i][j]) {j--;}   //这一列都比n大 (往左移动)
            else{ i++;}   //这一行都比n小(往下移动)
        }
        return false;
    }

}

实现结果

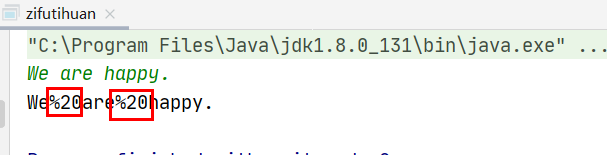
字符串

替换空格

面试四题目

请实现一个函数，把字符串中的每个空格替换成”%20”.例如输入“We are happy.”，则输出为”We%20are%20happy.”

题目分析

1. 这类题解决网络编程中由于URL参数中含有特殊字符导致服务器端无法获取正确的参数值。
    1.1 解决规则：通过在'%'后跟上ASCII码的两位十六进制的表示。
    1.2 解决举例：空格的ASCII码是32(16进制的0x20)，因此空格被替换为"%20"
2. 空格替换的实现方式：
    2.1 将原来的字符串中的空格字符 --> '%' '2' '0' 这三个字符(覆盖修改字符串后面的内存)
    2.2 新建StringBuilder字符串在此上面替换(可以自己分配足够多的内存) 
    2.3 新建数组实现

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public class zifutihuan {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        String s=input.nextLine();
        System.out.println(replaceSpace(s));
 System.out.println(replaceSpace(s));
    }

    //1.新建数组实现
    public static char[] replaceSpace(String s){
 		if(s==null){
            return null;  //字符串为空就输出null
        }
        char[] a=new char[s.length()*3];
        int size=0;
        //循环新字符数组然后进行更替操作
        for(int i=0;i<s.length();i++){
            char c=s.charAt(i);  //获取s字符串的对应字符
            if(c==' '){
                a[size++]='%';
                a[size++]='2';
                a[size++]='0';
            }else{
                a[size++]=c;  //把原来的字符放进去
            }
        }

      return a;
    }

    //2.新建StringBuilder类实现
    public String replaceSpace(StringBuffer str) {
    	if(str==null){
            return null;  //字符串为空就输出null
        }
        StringBuilder s=new StringBuilder();
        for(int i=0;i<str.length();i++){
            char c=str.charAt(i);
            if(c==' '){
                s.append('%');
                s.append('2');
                s.append('0');
            }else{
                 s.append(c);
            }
        }
        return s.toString();
    }

}

实现结果

字符串的排列

面试题二十八题目

题目分析

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class ZiFuPaiLie {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        String s=input.nextLine();
        System.out.println("要排列的字符串:"+s);
        System.out.println("排列之后的结果"+Permutation(s));
    }

    public static ArrayList<String> Permutation(String str) {
        ArrayList<String> ans=new ArrayList<String>();
        char[] a=str.toCharArray();  //字符串转数组
        
        return ans;
    }

}

实现结果

链表

从尾到头打印链表

面试五题目

输入一个链表的头结点，从尾到头反过来打印每个结点的值。

题目分析

1. 很明显这需要用栈实现，将链表的每个元素压入栈然后弹出

代码实现

ListNode类：

1
2
3
4
5
6
7
public class ListNode {
    int val;
    ListNode next;
    ListNode(int x) {
        val=x;
    }
}

mianshisan类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class mianshisan {
    public static void main(String[] args) {
        ListNode head1=new ListNode(1);
        ListNode head2=new ListNode(3);
        ListNode head3=new ListNode(2);
        head1.next=head2;  //生成链表：1 --> 2 --> 3
        head2.next=head3;
        head3.next=null;
       //调用方法
        reversePrint(head1);
    }

    //自定义反转打印的方法
    public static void reversePrint(ListNode head){
        //压栈
        Stack<ListNode> stk=new Stack<>();
        ListNode temp=head;
        while(temp!=null){  //直到指向最后一个位置
            stk.push(temp);
            temp=temp.next; //不断更替
        }
        //循环输出
        while(!stk.isEmpty()){
            System.out.println(stk.pop().val);  // 挨个出栈
        }
    }

}

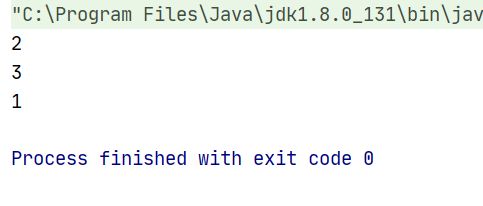
实现结果

树

重建二叉树

面试六题目

题目分析

此题就是

代码实现

1
2


实现结果

递归和循环

斐波那契数列

面试九题目

题目分析

1.递归：
    1.1 如果n=1/n=0就返回n
    1.2 其他情况下递归调用n-1和n-2

2.动态规划：    
    不断循环递进求最后一个数的原理
     c=a+b;  //第三个数
     a=b;   //原来的b成为下一轮的a
     b=c;   //原来的c成为下一轮的b

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public class FeiBo {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        int n=input.nextInt();
        //System.out.println("递归:"+digui(n));     //递归
        System.out.println("动态规划:"+dongtai(n));   //动态代理
    }

    //递归
    public static int digui(int n){
        if(n<=0){
            return 0;
        }
        if(n==1){
            return 1;
        }
        return digui(n-1)+digui(n-2);  //从第二项开始依次递增
    }

    //动态规划
    public static long  dongtai(int n){
		if(n<=0){
            return 0;
        }
        if(n<=2){
            return 1;
        }
        long a=1;
        long b=1;
        long c=2;
        for(int i=2;i<n;i++){  //依次往后挪动
            c=a+b;  //第三个数
            a=b;   //原来的b成为下一轮的a
            b=c;   //原来的c成为下一轮的b
        }
        return c;
    }

}

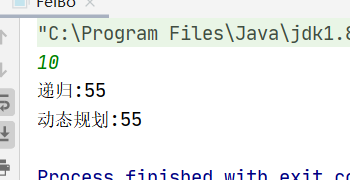
实现结果

1.测试小数字时候递归还可以：

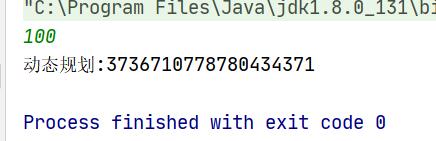
2.测试大的数字之后递归暴露了自己的缺点：

青蛙跳台阶(普通)

面试九题目

题目分析

1.递归
    1.1 前三项和n一样
    1.2 第四项之后开始就是前两项之和(斐波那契数列)
2.动态规划
    不断循环递进求最后一个数的原理
     c=a+b;  //第三个数
     a=b;   //原来的b成为下一轮的a
     b=c;   //原来的c成为下一轮的b

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import java.util.Scanner;
public class FeiBo {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        int n=input.nextInt();
        System.out.println("递归:"+digui(n));     //递归
        System.out.println("动态规划:"+dongtai(n));   //动态代理
    }

    //递归
    public static int digui(int n){
        if(n<=3){
            return n;  //前三个就是 1 2 3 (5 8...)
        }
        return digui(n-1)+digui(n-2);  //其余就是前两者之和
    }

    //动态规划
    public static long dongtai(int n) {
        if(n<=3){
            return n;  //前三个就是 1 2 3 (5 8...)
        }
        long sum=0;
        long a=1;
        long b=2;
        for(int i=2;i<n;i++){
            sum=a+b;  //后面的是前面的两次
            a=b;      //现在的第二个是下一轮的第一个
            b=sum;    //现在的总和是下一轮的第二个
        }
        return sum;
    }

}

实现结果

青蛙跳台阶(变态)

面试九题目

题目分析

 1.推理可得到f(n)=2f(n-1)

f(1) = 1;
f(2) = f(1)+1 = f(1)+f(1) = 2*f(1) = 2;
f(3) = f(2)+f(1)+1 = f(2)+f(1)+f(1)= f(2)+2*f(1) = f(2)+f(2)=2*f(2) = 2*2;
f(k) = f(k-1) + f(k-2) + …+ f(2)+ f(1) + 1= f(k-1) + f(k-2) + …+ f(3)+f(2)+f(1) + f(1)
     = 2*f(k-1)

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class QingWa {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        int n=input.nextInt();
        System.out.println("递归:"+tiao(n));       //递归
        System.out.println("动态规划:"+tiaoer(n)); //动态规划
    }

    //递归实现
    public static int tiao(int n) {
        if(n<=1){
            return 1;   // f(n)=1
        }
        return 2*tiao(n-1);  // f(n)=2*f(n-1)
    }

    //动态规划
     public static int tiaoer(int n) {
        if(n<=0){
            return 0;   // f(0)=0
        }
        if(n==1){
            return 1;   // f(1)=1
        }
        int a=1;
        int b=1;
        for(int i=1;i<n;i++){
            b=a*2;  //当前的值是上一个的二倍
            a=b;   //计算出来的值当做下一轮的数
        }
        return b;
    }

}

实现结果

位运算

二进制中1的个数

面试十题目

题目分析

1.关于求解1的个数(负数容易死循环--它要整体n/2右移保证还是一个负数所以前面一直补1--不可能将n/2为0)
    1.1 循环(只解决正数)：从个位不断取出来n(n%10)的数字判断是否为1然后n/n缩小范围最后输出个数
    1.2 位运算(n与n-1):会把最右边的1变为0 能进行多少次就相当于有多少个1
    1.3 使用Integer.toBinaryString(n)将n的二进制转为字符串，遍历1的个数

2.关于输出每位数字
    2.1 字符串拼接：(字符串+数字=数字拼一起)
    2.2 数组存放：(每一位放数组内反序输出)

代码实现(只能处理正数)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class QiuYi {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        int n=input.nextInt();
        System.out.println("一共有:"+qiu(n));  //1的个数
        System.out.println(qiuer(n));  //每一位的值
    }

    //求出有多少个1
    private static long qiu(int n) {
        long sum=0;  //计数器
        int m=1;  //每一位的值
        while(n!=0){
            m=n%2;
            if(m==1){
                sum++;  //如果是1就计数器加1
            }
            n=n/2;
        }
        return sum;
    }

    //输出每一位的值
    private static String qiuer(int n) {
        int[] a=new int[100];  //定义数组存放每一位元素
        String target="";
        int i=0;  //获取每一位的数字
        while(n!=0){
            i=n%2;
            target=i+target;  //字符串+数字=数字附加(将每次i放前面加  因为从个位取出来是反序的)
            n=n/2;
        }
        return target;
    }

}

代码实现(位运算)

1100为例，减去1就是1011，两者相与就是1000(相当于第二位的1没了)

1
2
3
4
5
6
7
8
private static int qiusan(int n) {
        int sum=0;
        while(n!=0){
            n=n&(n-1);  // (原整数-1)与(原整数) == (最右边1变为0)
            sum++;  //变一次就相当于记录一个1变化
        }
        return sum;
    }

代码实现(Integer.toBinaryString()然后遍历)

1
2
3
4
5
6
7
8
9
10
11
12
//Integer.toBinaryString()
    private static int qiusi(int n) {
        int sum=0;
        String s=Integer.toBinaryString(n);  //n的二进制转为字符串
        for(int i=0;i<s.length();i++){
            char c=s.charAt(i);  //取出每一个位置的字符
            if(c=='1'){
                sum++;  //字符如果为1计数器就加一
            }
        }
        return sum;
    }

实现结果

普通算法(只能解决正数 负数不能/2)

位运算(正负数均可)

易错面试题

数值的整数次方

面试十一题目

题目分析

1. 底为0   指数无论  --> 0
2. 底不为0 指数为0   --> 1
3. 底不为0 指数小于0 --> 按照循环求解之后答案取倒数
4. 底不为0 指数大于等于1 --> 正常流程

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public class CIFang {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        double n=input.nextDouble();
        int m=input.nextInt();
        System.out.println(n+"的"+m+"次方是"+cifang(n,m));
    }

    public static double cifang(double base,int exponent){
        double c=1;
        //底为0
        if(base==0){
            return 0;
        }
        if(exponent==0){  //任何数的0次方都是1
            return 1;
        }
        //底不为0  指数是负数
        if(exponent<0){
            exponent=-exponent;
            while (exponent--!=0) {  //有多少m就乘多少次n
                c*=base;  //c=c*n 在前面的基础上乘n
            }
            c=1.0/c;  //取倒数
        }
        //底不为o  指数大于等于1
        if(exponent>=1) {
            while (exponent--!=0) {  //有多少m就乘多少次n
                c*=base;  //c=c*n 在前面的基础上乘n
            }
        }
        return c;
    }

}

实现结果

打印1到最大的n位数

面试十二题目

题目分析

1. 暴力法(无法解决大数问题)：先算出最大值，然后按序输出
2. 数组/字符串：
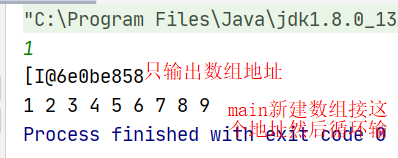
3. 全排列：

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//1.暴力法(找到最大数然后按序输出)
   public static String printNumbers(int n){  //传入一个n
       int max=0;  //输出的最大的值
       //1.先求出最大数(方便定义数组下标大小)
       for(int i=0;i<n;i++){
           max=max*10+9;    //从9 99 999 9999...
       }
       //2.通过最大值创建数组
       int[] a=new int[max];
       for(int i=1;i<=max;i++){
               a[i]=i;
       }
       return Arrays.toString(a);  //使用Arrays的方法将数组转为字符串
   }

实现结果

数组中只出现一次的数字

题目

题目分析

1. 使用数组下标的好处：新建数组记录下标计数
2. 使用set集合(不能重复)：然后将1次以上的直接弹出，其他的添加到set集合

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class YiCi {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        int n=input.nextInt();
        int[] a=new int[n];
        for(int i=0;i<a.length;i++){
            a[i]=input.nextInt();  //输入要判断的数组元素
        }
        System.out.println(Find(a));
    }

    public static Set<Integer> Find(int[] a) {
        Set<Integer> s1=new HashSet<>();
        for(int i=0;i<a.length;i++){
            if(!s1.add(a[i])){  //如果重复了(2次以上)
                s1.remove(a[i]);  //移除set集合 里面剩下的就都是只出现一次的值
            }
        }
        return s1;
    }

}

实现结果

调整数组顺序(奇数在偶数前面)

面试十四题目

题目分析

思路：使用两个指针交换奇偶数(快排的感觉)
    1. 左右指针赋初始值
    2. 分下面三种情况
        2.1 左指针不超过右指针 + 左边值是奇数(不需要交换) --> 左指针右移
        2.2 左指针不超过右指针 + 右边值是偶数(不需要交换) --> 右指针左移
        2.3 其他情况下直接交换左右指针对应数组的值

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class ShunXu {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        int n=input.nextInt();  //输入二维数组的行和列
        int m=input.nextInt();
        int[][] a=new int[n][m];
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i][j]=input.nextInt();  //输入要判断的数组元素
            }
        }


    }

    public static ArrayList<Integer> printMatrix(int [][] matrix) {
        ArrayList<Integer> list=new ArrayList<Integer>();  //定义arraylist集合 底层是数组
        int row=matrix.length;     //行
        int col=matrix[0].length;  //列
        int left=0;
        int right=col-1;
        int top=0;
        int bottom=row-1;
        return list;
    }

}

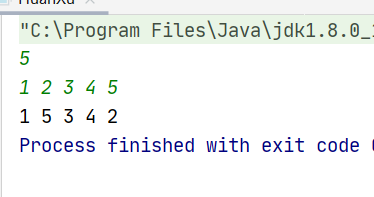
实现结果

顺时针打印矩阵

面试二十题目

题目分析

1. 如果数组为空 --返回为null
2. 如果数组不为空
     2.1 建立ArrayList集合
     2.2 建立四个坐标用于标识数组变化
     2.3 从左往右(行：top    列：left到right)
     2.4 从上到下(行：top+1到bottom  列：right) 
     2.5 从右到左(行：bottom  列：right-1到left)  --但要注意可能最后是一行就不需要进行这一步
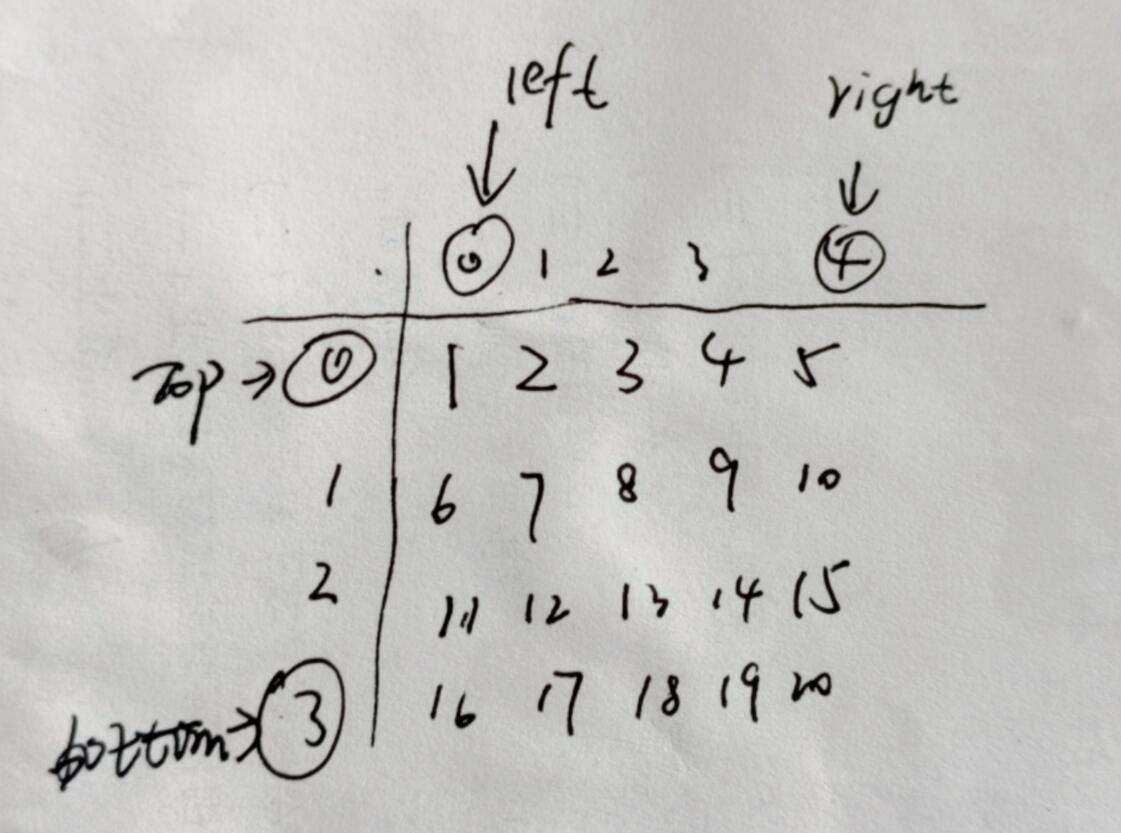
     2.6 从下到上(行：bottom-1到top  列：left)    --但要注意可能最后是一列就不需要进行这一步

关于left/right/bottom/top的分析：

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public class ShunXu {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        int n=input.nextInt();  //输入二维数组的行和列
        int m=input.nextInt();
        int[][] a=new int[n][m];
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i][j]=input.nextInt();  //输入要判断的数组元素
            }
        }

        System.out.println(printMatrix(a));  //打印调用方法结果
    }

    public static ArrayList<Integer> printMatrix(int [][] matrix) {
        if(matrix==null){
            return null;  //如果数组为空 就输出null
        }
        ArrayList<Integer> list=new ArrayList<Integer>();  //定义arraylist集合 底层是数组
        int row=matrix.length;     //行
        int col=matrix[0].length;  //列
        int left=0;   //二维数组上面行的最左边
        int right=col-1; //二维数组上面行的最右边
        int top=0;   //二维数组左边的最上边
        int bottom=row-1;  //二维数组左边的最下边
        while(left<=right&&top<=bottom){
            //从左到右
            for(int i=left;i<=right;i++){
                list.add(matrix[top][i]);
            }
            //从上到下(从下一行开始向下走)
            for(int i=top+1;i<=bottom;i++){
                list.add(matrix[i][right]);
            }
            //从右到左(从左边一列开始向左走)
            if(top!=bottom) {   //如果是一行的话就不需要返回去(已经左到右)
                for (int i = right - 1; i >= left; i--) {
                    list.add(matrix[bottom][i]);
                }
            }
            //从下到上(从上一行开始向上走)
            if(left!=right) {  //如果是一列的话就不需要返回去(已经上到下)
                for (int i = bottom - 1; i > top; i--) {
                    list.add(matrix[i][left]);
                }
            }
            //下一个正方形矩阵(往里缩小 -- 变换四个下标)
            top++;
            right--;
            left++;
            bottom--;
        }
        return list;
    }

}

实现结果

赏

×

纯属好玩

扫码支持
扫码打赏，你说多少就多少

打开支付宝扫一扫，即可进行扫码打赏哦

本文标题:剑指offer

文章作者:Larkkkkkkk

发布时间:2020年05月11日 - 22时51分

最后更新:2020年06月01日 - 15时56分

原始链接:https://larkkkkkkk.github.io/2020/05/11/%E5%89%91%E6%8C%87offer/

许可协议: "署名-非商用-相同方式共享 3.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 数组
    1. 1.1. 二维数组的查找
      1. 1.1.1. 面试三题目
      2. 1.1.2. 题目分析
      3. 1.1.3. 代码实现
      4. 1.1.4. 实现结果
  2. 2. 字符串
    1. 2.1. 替换空格
      1. 2.1.1. 面试四题目
      2. 2.1.2. 题目分析
      3. 2.1.3. 代码实现
      4. 2.1.4. 实现结果
    2. 2.2. 字符串的排列
      1. 2.2.1. 面试题二十八题目
      2. 2.2.2. 题目分析
      3. 2.2.3. 代码实现
      4. 2.2.4. 实现结果
  3. 3. 链表
    1. 3.1. 从尾到头打印链表
      1. 3.1.1. 面试五题目
      2. 3.1.2. 题目分析
      3. 3.1.3. 代码实现
      4. 3.1.4. 实现结果
  4. 4. 树
    1. 4.1. 重建二叉树
      1. 4.1.1. 面试六题目
      2. 4.1.2. 题目分析
      3. 4.1.3. 代码实现
      4. 4.1.4. 实现结果
  5. 5. 递归和循环
    1. 5.1. 斐波那契数列
      1. 5.1.1. 面试九题目
      2. 5.1.2. 题目分析
      3. 5.1.3. 代码实现
      4. 5.1.4. 实现结果
    2. 5.2. 青蛙跳台阶(普通)
      1. 5.2.1. 面试九题目
      2. 5.2.2. 题目分析
      3. 5.2.3. 代码实现
      4. 5.2.4. 实现结果
    3. 5.3. 青蛙跳台阶(变态)
      1. 5.3.1. 面试九题目
      2. 5.3.2. 题目分析
      3. 5.3.3. 代码实现
      4. 5.3.4. 实现结果
  6. 6. 位运算
    1. 6.1. 二进制中1的个数
      1. 6.1.1. 面试十题目
      2. 6.1.2. 题目分析
      3. 6.1.3. 代码实现(只能处理正数)
      4. 6.1.4. 代码实现(位运算)
      5. 6.1.5. 代码实现(Integer.toBinaryString()然后遍历)
      6. 6.1.6. 实现结果
  7. 7. 易错面试题
    1. 7.1. 数值的整数次方
      1. 7.1.1. 面试十一题目
      2. 7.1.2. 题目分析
      3. 7.1.3. 代码实现
      4. 7.1.4. 实现结果
    2. 7.2. 打印1到最大的n位数
      1. 7.2.1. 面试十二题目
      2. 7.2.2. 题目分析
      3. 7.2.3. 代码实现
      4. 7.2.4. 实现结果
    3. 7.3. 数组中只出现一次的数字
      1. 7.3.1. 题目
      2. 7.3.2. 题目分析
      3. 7.3.3. 代码实现
      4. 7.3.4. 实现结果
    4. 7.4. 调整数组顺序(奇数在偶数前面)
      1. 7.4.1. 面试十四题目
      2. 7.4.2. 题目分析
      3. 7.4.3. 代码实现
      4. 7.4.4. 实现结果
    5. 7.5. 顺时针打印矩阵
      1. 7.5.1. 面试二十题目
      2. 7.5.2. 题目分析
      3. 7.5.3. 代码实现
      4. 7.5.4. 实现结果
,