二叉树(任何子节点数<=2)
1. 最大度为2
2. 可以为空
3. 有序树(左右节点不同)
存储方式
1. 链式存储
2. 顺序存储
满二叉树(很完美)
最层都是最饱满的样子
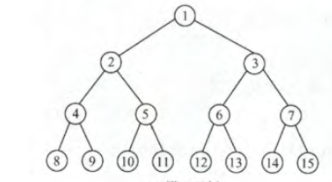
完全二叉树(编号没有间断)
编号连续的满二叉树的子集
二叉树链式存储
实现功能
1. 前/中/后序遍历
2. 前/中/后序查找 (当前满足/左节点满足/右节点满足)
3. 删除子树【递归】 (当前节点可删/左节点/右节点)
三种遍历方法解析
不断递归自己的方法遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| // 前序遍历(根左右)
public void frontShow() {
System.out.print(value+" "); //先输出当前节点内容
if (leftNode != null) {
leftNode.frontShow(); //左节点
}
if (rightNode != null) {
rightNode.frontShow(); //右节点
}
}
// 中序遍历(左根右)
public void midShow() {
if (leftNode != null) {
leftNode.midShow(); //左节点
}
System.out.print(value+" "); //先输出当前节点内容
if (rightNode != null) {
rightNode.midShow(); //右节点
}
}
//后序遍历(左右根)
public void afterShow() {
if (leftNode != null) {
leftNode.midShow(); //左节点
}
if (rightNode != null) {
rightNode.midShow(); //右节点
}
System.out.print(value+" "); //先输出当前节点内容
}
|
查找节点
判断节点的value值和查找的i是否相等
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| //前序查找
public TreeNode frontSerach(int i){
TreeNode target=null;
if(this.value==i) {
return this; //当前节点的值就是要查找的值
}else{
if(leftNode!=null){
target=leftNode.frontSerach(i); //左边的值查到的话给target
}
if(target!=null){
return target; //如果查到了就不为空 返回target
}
if(rightNode!=null){
target=rightNode.frontSerach(i); //右边的值可以查到
}
}
return target;
}
|
删除子树
如果是根节点直接为null/其他的话就不断递归判断左右节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| //删除子树
public void delete(int i) {
TreeNode parent=this; //把上一层节点存起来
if(parent.leftNode!=null&&parent.leftNode.value==i){ //左节点是这个值
parent.leftNode=null; ///这个节点置空
return;
}
if(parent.rightNode!=null&&parent.rightNode.value==i){ //右节点是这个值
parent.rightNode=null; //这个节点置空
return;
}
parent=leftNode; //左边节点给上一层节点 递归
if(parent!=null){
parent.delete(i);
}
parent=rightNode; //右边节点给上一层节点 递归
if(parent!=null){
parent.delete(i);
}
}
|
完整代码
1. BinaryTree类 :创建树(set/get方法) 所需要的方法定义(调用TreeNode方法)
2. TreeNode类 : 描述节点权和左右儿子(方法具体实现)
3. TestBinaryTree类 :创建树添加节点
BinaryTree类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| public class BinaryTree {
TreeNode root;
//设置根节点
public void setRoot(TreeNode root) {
this.root = root;
}
//获取根节点
public TreeNode getRoot() {
return root;
}
//前序遍历
public void frontShow(){
if(root!=null){
root.frontShow(); //其实就是去TreeNode里面实现
}
}
//中序遍历
public void midShow(){
if(root!=null) {
root.midShow(); //其实就是去TreeNode里面实现
}
}
//后序遍历
public void afterShow() {
if (root != null) {
root.afterShow(); //其实就是去TreeNode里面实现
}
}
//前序查找
public TreeNode frontSearch(int i){
return root.frontSerach(i);
}
//删除子树
public void delete(int i) {
if(root.value==i){
root=null; //当前的节点值刚好是要删除的 直接为null
}else{
root.delete(i); //删除节点
}
}
}
|
TreeNode类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
| public class TreeNode {
//节点的权
int value;
//左儿子
TreeNode leftNode;
//右儿子
TreeNode rightNode;
public void setLeftNode(TreeNode leftNode) {
this.leftNode = leftNode;
}
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
public TreeNode(int value){
this.value=value;
}
// 前序遍历(根左右)
public void frontShow() {
System.out.print(value+" "); //先输出当前节点内容
if (leftNode != null) {
leftNode.frontShow(); //左节点
}
if (rightNode != null) {
rightNode.frontShow(); //右节点
}
}
// 中序遍历(左根右)
public void midShow() {
if (leftNode != null) {
leftNode.midShow(); //左节点
}
System.out.print(value+" "); //先输出当前节点内容
if (rightNode != null) {
rightNode.midShow(); //右节点
}
}
//后序遍历(左右根)
public void afterShow() {
if (leftNode != null) {
leftNode.midShow(); //左节点
}
if (rightNode != null) {
rightNode.midShow(); //右节点
}
System.out.print(value+" "); //先输出当前节点内容
}
//前序查找
public TreeNode frontSerach(int i){
TreeNode target=null;
if(this.value==i) {
return this; //当前节点的值就是要查找的值
}else{
if(leftNode!=null){
target=leftNode.frontSerach(i); //左边的值查到的话给target
}
if(target!=null){
return target; //如果查到了就不为空 返回target
}
if(rightNode!=null){
target=rightNode.frontSerach(i); //右边的值可以查到
}
}
return target;
}
//删除子树
public void delete(int i) {
TreeNode parent=this; //把上一层节点存起来
if(parent.leftNode!=null&&parent.leftNode.value==i){ //左节点是这个值
parent.leftNode=null;
return;
}
if(parent.rightNode!=null&&parent.rightNode.value==i){ //右节点是这个值
parent.rightNode=null;
return;
}
parent=leftNode; //左边节点给上一层节点 递归
if(parent!=null){
parent.delete(i);
}
parent=rightNode; //右边节点给上一层节点 递归
if(parent!=null){
parent.delete(i);
}
}
}
|
TestBinaryTree类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| public class TestBinaryTree {
public static void main(String[] args) {
//创建一棵树
BinaryTree binTree=new BinaryTree();
//创建一个根节点
TreeNode root=new TreeNode(1);
//根节点赋给树
binTree.setRoot(root); //根节点赋给树
//创建两个节点
TreeNode rootL=new TreeNode(2); //创建第二层的2
TreeNode rootR=new TreeNode(3); //创建第二层的3
//新节点设置为根的两个节点
root.setLeftNode(rootL);
root.setRightNode(rootR);
//给根的左节点2创建两个节点
rootL.setLeftNode(new TreeNode(4));
rootL.setRightNode(new TreeNode(5));
//给根的右节点3创建两个节点
rootR.setLeftNode(new TreeNode(6));
rootR.setRightNode(new TreeNode(7));
//前序遍历
System.out.print("前序遍历:");
binTree.frontShow();
System.out.println();
//中序遍历
System.out.print("中序遍历:");
binTree.midShow();
System.out.println();
//后序遍历
System.out.print("后序遍历:");
binTree.afterShow();
System.out.println();
//前序查找
TreeNode result=binTree.frontSearch(3);
System.out.println("前序查找结果:"+result);
//删除子树(切点上层节点和它的关系)
binTree.delete(2);
binTree.frontShow();
}
}
|
执行结果:

二叉树顺序存储
只考虑完全二叉树(编号连续)
顺序存储的性质
1. 第n个元素的左子节点 : 2*n+1
2. 第n个元素的右子节点 : 2*n+2
3. 任何一个节点的父节点 : (n-1)/2
具体类(三种遍历)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| public class ArrayBinaryTree {
int[] data; //定义一个数组用于后面方法实现
public ArrayBinaryTree(int[] data){ //构造方法传入数组
this.data=data;
}
public void frontShow(){
frontShow(0);
}
//前序遍历
public void frontShow(int i){
if(data==null||data.length==0){
return; //如果数组为空或者长度为0就输出0
}
System.out.println(data[i]); // 输出当前的节点 (根)
if(2*i+1<data.length){
frontShow(2*i+1); //递归 找左节点(2n+1)
}
if(2*i+2<data.length){
frontShow(2*i+2); //递归 找右节点(2n+2)
}
}
}
|
测试类
1
2
3
4
5
6
7
8
| public class Shunxu {
public static void main(String[] args) {
int[] data=new int[]{1,2,3,4,5,6,7}; //定义一个链表存储的在数组内
ArrayBinaryTree tree=new ArrayBinaryTree(data); //传入数组
tree.frontShow(); //前序遍历
}
}
|
结果:

线索二叉树(双向链表)
线索二叉树概念:
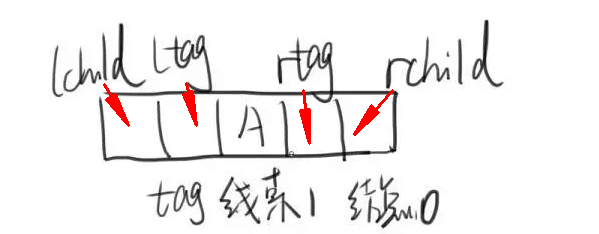
1. 一个节点的前一个节点 --> 前驱节点(左边标记为lflag)
2. 一个节点的后一个节点 --> 后继节点(右边标记为rflag)
具体实现(可知前后节点信息)
中序线索化二叉树(关键点)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| //中序线索化二叉树
//用于临时存储前驱结点
ThreadedNode pre=null;
public void threadNodes(){
threadNodes(root); //通过root不停的递归
}
public void threadNodes(ThreadedNode node){
//1. 当前节点如果为null 直接返回
if(node==null){
return;
}
//2. 处理左子树
threadNodes(node.leftNode);
//2.1 如果当前节点没有了 我们处理它的前驱节点
if (node.leftNode == null) {
node.leftNode=pre; //当前节点的左指针 指向 前驱节点
node.leftType=1; // 当前节点的左指针类型从0 -> 1
}
//2.2 前驱结点的右指针 如果是null(没有指向右下子树)
if(pre!=null&&pre.rightNode==null){
pre.rightNode=node;
pre.rightType=1;
}
//2.3 每次处理一个节点,当前节点就是下一个节点的前驱节点(依次往下走 下一个的上面就是上一个)
pre=node;
//3. 处理右子树
threadNodes(node.rightNode);
}
|
遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public void threadIterate(){
ThreadedNode node=root;
while(node!=null){
//循环找到最开始的节点
while(node.leftType==0){
node=node.leftNode;
}
System.out.println(node.value); //打印当前节点的值
//如果当前节点的右节点是后继节点,有可能后继节点还有后继节点
while(node.rightType==1){
node=node.rightNode;
System.out.println(node.value);
}
node=node.rightNode; //替换遍历的节点
}
}
|
完整代码如下(三个类)
ThreadedBinaryTree类(二叉树的基础上添加中序线索树和遍历的方法)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
| public class ThreadedBinaryTree {
ThreadedNode root;
//设置根节点
public void setRoot(ThreadedNode root) {
this.root = root;
}
//获取根节点
public ThreadedNode getRoot() {
return root;
}
//中序线索化二叉树
//用于临时存储前驱结点
ThreadedNode pre=null;
public void threadNodes(){
threadNodes(root); //通过root不停的递归
}
public void threadNodes(ThreadedNode node){
//1. 当前节点如果为null 直接返回
if(node==null){
return;
}
//2. 处理左子树
threadNodes(node.leftNode);
//2.1 如果当前节点没有了 我们处理它的前驱节点
if (node.leftNode == null) {
node.leftNode=pre; //当前节点的左指针 指向 前驱节点
node.leftType=1; // 当前节点的左指针类型从0 -> 1
}
//2.2 前驱结点的右指针 如果是null(没有指向右下子树)
if(pre!=null&&pre.rightNode==null){
pre.rightNode=node;
pre.rightType=1;
}
//2.3 每次处理一个节点,当前节点就是下一个节点的前驱节点(依次往下走 下一个的上面就是上一个)
pre=node;
//3. 处理右子树
threadNodes(node.rightNode);
}
//遍历线索二叉树
public void threadIterate(){
ThreadedNode node=root;
while(node!=null){
//循环找到最开始的节点
while(node.leftType==0){
node=node.leftNode;
}
System.out.println(node.value); //打印当前节点的值
//如果当前节点的右节点是后继节点,有可能后继节点还有后继节点
while(node.rightType==1){
node=node.rightNode;
System.out.println(node.value);
}
node=node.rightNode; //替换遍历的节点
}
}
//前序遍历
public void frontShow(){
if(root!=null){
root.frontShow(); //其实就是去TreeNode里面实现
}
}
//中序遍历
public void midShow(){
if(root!=null) {
root.midShow(); //其实就是去TreeNode里面实现
}
}
//后序遍历
public void afterShow() {
if (root != null) {
root.afterShow(); //其实就是去TreeNode里面实现
}
}
//前序查找
public ThreadedNode frontSearch(int i){
return root.frontSerach(i);
}
//删除子树
public void delete(int i) {
if(root.value==i){
root=null; //当前的节点值刚好是要删除的 直接为null
}else{
root.delete(i); //删除节点
}
}
}
|
TestThreadedBinaryTree测试类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| public class TestThreadedBinaryTree {
public static void main(String[] args) {
//创建一棵树
ThreadedBinaryTree binTree=new ThreadedBinaryTree();
//创建一个根节点
ThreadedNode root=new ThreadedNode(1);
//根节点赋给树
binTree.setRoot(root); //根节点赋给树
//创建两个节点
ThreadedNode rootL=new ThreadedNode(2); //创建第二层的2
ThreadedNode rootR=new ThreadedNode(3); //创建第二层的3
//新节点设置为根的两个节点
root.setLeftNode(rootL);
root.setRightNode(rootR);
//给根的左节点2创建两个节点
rootL.setLeftNode(new ThreadedNode(4));
ThreadedNode fiveNode=new ThreadedNode(5);
rootL.setRightNode(fiveNode);
//给根的右节点3创建两个节点
rootR.setLeftNode(new ThreadedNode(6));
rootR.setRightNode(new ThreadedNode(7));
//中序遍历
System.out.print("中序遍历:");
binTree.midShow();
System.out.println();
System.out.println("---------------");
//中序线索二叉树
System.out.print("5后面的节点:");
binTree.threadNodes();
//查看5的后继节点
ThreadedNode after=fiveNode.rightNode;
System.out.println(after.value);
binTree.threadIterate(); //测试遍历
}
}
|
ThreadedNode节点类(只需要添加左右指针类型)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
| public class ThreadedNode {
//节点的权
int value;
//左儿子
ThreadedNode leftNode;
//右儿子
ThreadedNode rightNode;
//用于标识指针类型
int leftType;
int rightType;
public void setLeftNode(ThreadedNode leftNode) {
this.leftNode = leftNode;
}
public void setRightNode(ThreadedNode rightNode) {
this.rightNode = rightNode;
}
public ThreadedNode(int value){
this.value=value;
}
// 前序遍历(根左右)
public void frontShow() {
System.out.print(value+" "); //先输出当前节点内容
if (leftNode != null) {
leftNode.frontShow(); //左节点
}
if (rightNode != null) {
rightNode.frontShow(); //右节点
}
}
// 中序遍历(左根右)
public void midShow() {
if (leftNode != null) {
leftNode.midShow(); //左节点
}
System.out.print(value+" "); //先输出当前节点内容
if (rightNode != null) {
rightNode.midShow(); //右节点
}
}
//后序遍历(左右根)
public void afterShow() {
if (leftNode != null) {
leftNode.midShow(); //左节点
}
if (rightNode != null) {
rightNode.midShow(); //右节点
}
System.out.print(value+" "); //先输出当前节点内容
}
//前序查找
public ThreadedNode frontSerach(int i){
ThreadedNode target=null;
if(this.value==i) {
return this; //当前节点的值就是要查找的值
}else{
if(leftNode!=null){
target=leftNode.frontSerach(i); //左边的值查到的话给target
}
if(target!=null){
return target; //如果查到了就不为空 返回target
}
if(rightNode!=null){
target=rightNode.frontSerach(i); //右边的值可以查到
}
}
return target;
}
//删除子树
public void delete(int i) {
ThreadedNode parent=this; //把上一层节点存起来
if(parent.leftNode!=null&&parent.leftNode.value==i){ //左节点是这个值
parent.leftNode=null;
return;
}
if(parent.rightNode!=null&&parent.rightNode.value==i){ //右节点是这个值
parent.rightNode=null;
return;
}
parent=leftNode; //左边节点给上一层节点 递归
if(parent!=null){
parent.delete(i);
}
parent=rightNode; //右边节点给上一层节点 递归
if(parent!=null){
parent.delete(i);
}
}
}
|
结果:

二叉排序树BST(二叉查找树/二叉搜索树)
任何一个非叶子节点 : 左子节点<当前节点<右子节点
具体实现的代码框架
1. BinarySortTree类 : 一个root根节点 然后围绕写方法
2. Node节点类 : 具体方法实现
3. TestBinarySortTree测试类 : 测试结果
创建二叉排序树(添加节点)
实现思路
1. 空树 -- 直接让要添加的节点成为root根节点
2. 不为空树 -- 调用Node实现方法
2.1 要添加的节点为空 -- 直接返回
2.2 要添加的节点的值 < 当前节点的值
2.2.1 当前节点有左节点 -- 继续递归找
2.2.2 当前节点下面空 -- 直接添加到左节点的位置
2.2 要添加的节点的值 > 当前节点的值
2.2.1 当前节点有右节点 -- 继续递归找
2.2.2 当前节点下面空 -- 直接添加到右节点的位置
BinarySortTree类写方法
1
2
3
4
5
6
7
8
9
10
11
12
|
//向二叉排序树中添加节点
public void add(Node node){
//1. 如果是空树
if(root==null){
root=node; //这个节点添加为根节点
}
//2. 不是空树
else{
root.add(node); //调用Node类的方法添加
}
}
|
Node类具体实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| //向子树中添加节点
public void add(Node node) {
//1.传入的节点为空
if(node==null){
return; //直接结束
}
//2.传入的节点的值和当前子树的根节点大小关系
//2.1 传入节点值 < 子树的根节点的值
if(node.value<this.value) {
//2.1.1 当前子树的根节点下面没有左子树 -- 直接添加
if(this.left==null){
this.left=node; //直接添加到左节点
//2.1.2 当前子树的根节点下面有左子树 -- 需要递归去找到
}else{
this.left.add(node); // 在当前子树的根节点下面的左节点下面去添加 (递归)
}
}
//2.2 传入节点值 > 子树的根节点的值
else{
//2.1.1 当前子树的根节点下面没有左子树 -- 直接添加
if(this.right==null){
this.right=node; //直接添加到左节点
//2.1.2 当前子树的根节点下面有左子树 -- 需要递归去找到
}else{
this.right.add(node); // 在当前子树的根节点下面的左节点下面去添加 (递归)
}
}
}
|
查找节点
实现思路
1. 空树 -- 返回null
2. 不为空树 -- 调用Node实现方法
2.1 传入的值 == 当前节点值 -- 返回当前节点
2.2 传入的值 < 当前节点值 -- 找左边
2.2.1 如果左边为空 -- 返回null
2.2.2 如果左边不为空 -- 把左节点当做判断的当前节点(递归)
2.3 传入的值 > 当前节点值 -- 找右边
2.3.1 如果右边为空 -- 返回null
2.3.2 如果右边不为空 -- 把右节点当做判断的当前节点(递归)
BinarySortTree类写方法
1
2
3
4
5
6
7
8
9
10
11
| //查找
public Node search(int value){
//1. 如果空树 -- 返回null
if(root==null){
return null;
}
//2. 如果不为空
else{
return root.search(value);
}
}
|
Node类具体实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| //查找节点
public Node search(int value) {
//1. 传入的值 == 当前节点值
if(this.value==value){
return this; //返回当前节点
}
//2. 传入的值 < 当前节点值 -- 找左边
else if(value<this.value){
if(left==null){return null;} //为空返回null
return this.left.search(value);
}
//3. 传入的值 > 当前节点值 -- 找右边
else{
if(right==null){return null;} //为空返回null
return this.right.search(value);
}
}
|
测试添加节点和查询功能
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public class TestBinarySortTree {
public static void main(String[] args) {
int[] arr=new int[]{7,3,10,12,5,1,9};
//1. 创建一颗二叉排序树
BinarySortTree bst=new BinarySortTree();
//2. 循环添加
for(int i:arr){
bst.add(new Node(i));
}
//3. 中序遍历
bst.midShow();
System.out.println("----------------------");
//4. 查找数中的值
Node node = bst.search(10);
System.out.println("查找值为10的节点的值 : "+node.value);
Node node2 = bst.search(20);
System.out.println("查找值为20的节点是不是为空 : "+node2);
System.out.println("查找值为20的节点的值 : "+node2.value);
}
}
|
测试结果:
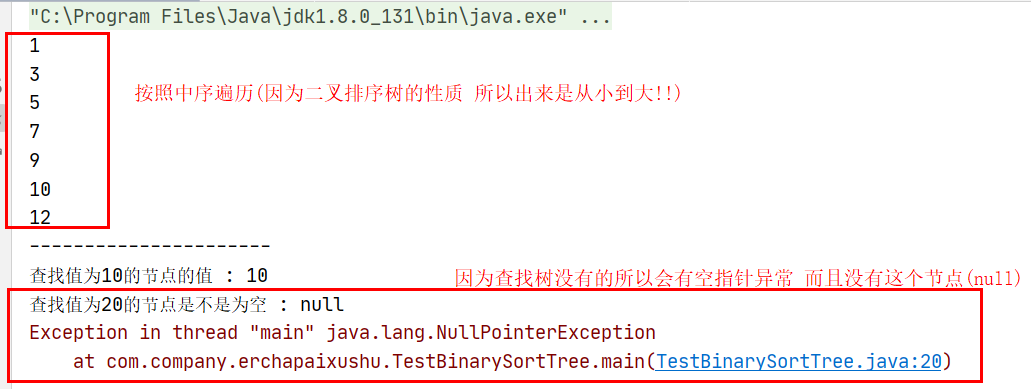
删除节点
三种情况概述
1. 删除叶子节点(两种情况): 让父节点不指向它(左边/右边)
2. 删除有一颗子树的节点(四种情况): 让它的子树代替它的位置(它在左/右边 子树在左/右边)
3. 删除有两颗子树的节点(两种情况):
1. 找到右边最小的替换掉删除的点(它没有叶子节点)
2. 找到右边最小的替换掉删除的点+右节点替换掉最小的点的位置 (它有右节点(左节点的话就是第一种情况))
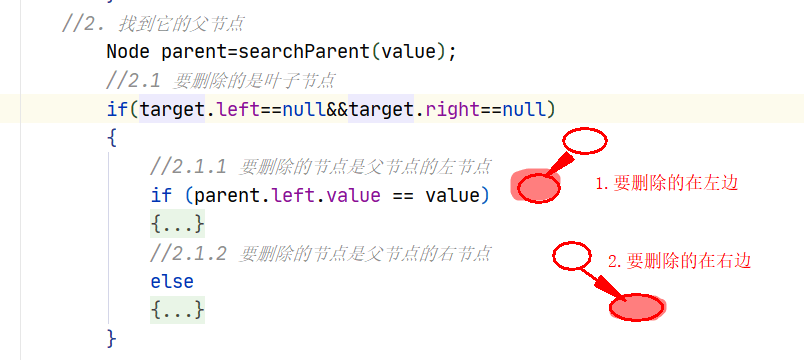
删除叶子节点(2种情况)
实现思路
1. 删除的叶子节点是左节点 -- 让父节点的左节点为空
2. 删除的叶子节点是右节点 -- 让父节点的右节点为空
图示解释
BinarySortTree类写方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
if(target.left==null&&target.right==null)
{
//2.1.1 要删除的节点是父节点的左节点
if (parent.left.value == value)
{
parent.left = null; //直接让父节点把它为null
}
//2.1.2 要删除的节点是父节点的右节点
else
{
parent.right = null; //直接让父节点把它为null
}
}
|
Node类具体实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| //查找父节点
public Node searchParent(int value) {
if((this.left!=null&&this.left.value==value)||(this.right!=null&&this.right.value==value)){
return this;
}else {
if(this.value>value&&this.left!=null){
return this.left.searchParent(value);
}else
if(this.value<value&&this.right!=null){
return this.right.searchParent(value);
}
}
return null;
}
|
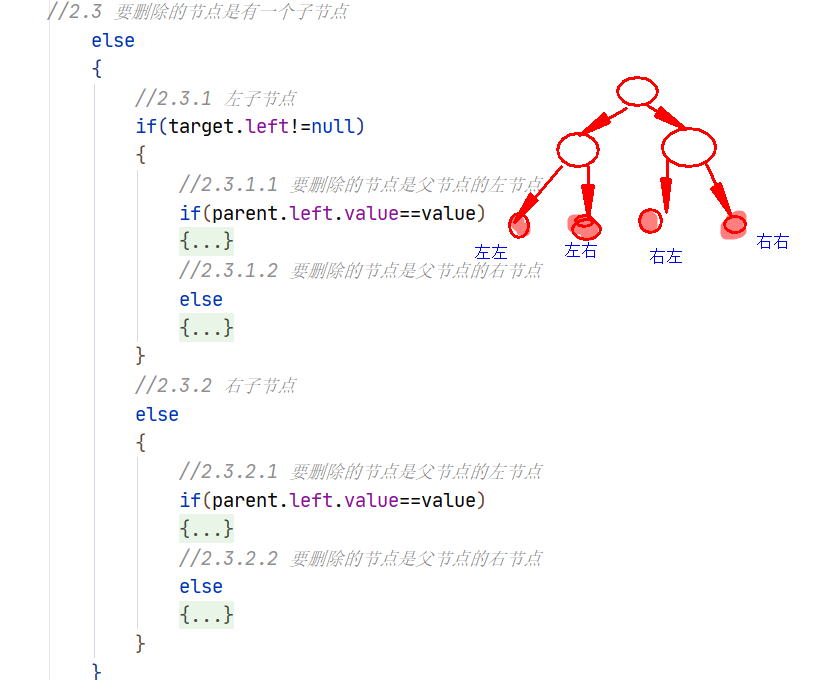
删除有一颗子树的节点(4种情况)
实现思路
1. 删除的节点是父节点的左/右节点? 删除的节点的子节点是左/右节点?
1.1 要删除的节点有的是左子节点
1.1.1 要删除的节点是父节点的左节点(左左) -- 将删除节点的左节点赋给父节点的左节点
1.1.2 要删除的节点是父节点的右节点(右左) -- 将删除节点的左节点赋给父节点的右节点
1.2 要删除的节点有的是右子节点
1.2.1 要删除的节点是父节点的左节点(左右) -- 将删除节点的右节点赋给父节点的左节点
1.2.2 要删除的节点是父节点的右节点(右右) -- 将删除节点的右节点赋给父节点的右节点
图示解释
BinarySortTree类写方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
//2.3.1 左子节点
if(target.left!=null)
{
//2.3.1.1 要删除的节点是父节点的左节点
if(parent.left.value==value)
{
parent.left=target.left; //要删除的是父节点的左节点 然后它有的是左节点
}
//2.3.1.2 要删除的节点是父节点的右节点
else
{
parent.right=target.left; //要删除的是父节点的右节点 然后它有的是左节点
}
}
//2.3.2 右子节点
else
{
//2.3.2.1 要删除的节点是父节点的左节点
if(parent.left.value==value)
{
parent.left=target.right; //要删除的是父节点的右节点 然后它有的是左节点
}
//2.3.2.2 要删除的节点是父节点的右节点
else
{
parent.right=target.right; //要删除的是父节点的右节点 然后它有的是右节点
}
}
|
删除有两颗子树的节点(2种情况)
1. 右边最小值有没有子节点?
1.1 右边最小值没有子节点 -- 直接将最小值的节点值赋给要删除的节点的值
1.1 右边最小值有子节点(只有右节点) -- 直接将最小值的节点值赋给要删除的节点的值 +子节点的值赋给最小值的节点值
实现思路
BinarySortTree类写方法
1
2
3
4
5
6
7
| if(target.left!=null&&target.right!=null)
{
//2.2.1 删除右子树最小的节点并且获取到该节点的值
int min=deleteMin(target.right);
//2.2.2 替换目标节点中的值
target.value=min; //最小的值赋给要删除的节点的值
}
|
完整代码
BinarySortTree类写方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
| package com.company.erchapaixushu;
public class BinarySortTree {
//root根节点
Node root;
//向二叉排序树中添加节点
public void add(Node node){
//1. 如果是空树
if(root==null){
root=node; //这个节点添加为根节点
}
//2. 不是空树
else{
root.add(node); //调用Node类的方法添加
}
}
//中序遍历(刚好是从小到大)
public void midShow(){
if(root!=null){
root.midShow(root); //查找这个根节点开始的中序遍历
}
}
//查找节点
public Node search(int value){
//1. 如果空树 -- 返回null
if(root==null){
return null;
}
//2. 如果不为空
else{
return root.search(value);
}
}
//删除节点
public void delete(int value){
if(root==null)
{
return; //空树直接返回
}
else
{
//1. 找到这个节点
Node target = search(value);
if(target==null)
{
return;
}
//2. 找到它的父节点
Node parent=searchParent(value);
//2.1 要删除的是叶子节点
if(target.left==null&&target.right==null)
{
//2.1.1 要删除的节点是父节点的左节点
if (parent.left.value == value)
{
parent.left = null; //直接让父节点把它为null
}
//2.1.2 要删除的节点是父节点的右节点
else
{
parent.right = null; //直接让父节点把它为null
}
}
//2.2 要删除的节点有两个子节点
else
if(target.left!=null&&target.right!=null)
{
//2.2.1 删除右子树最小的节点并且获取到该节点的值
int min=deleteMin(target.right);
//2.2.2 替换目标节点中的值
target.value=min;
}
//2.3 要删除的节点是有一个子节点
else
{
//2.3.1 左子节点
if(target.left!=null)
{
//2.3.1.1 要删除的节点是父节点的左节点
if(parent.left.value==value)
{
parent.left=target.left; //要删除的是父节点的左节点 然后它有的是左节点
}
//2.3.1.2 要删除的节点是父节点的右节点
else
{
parent.right=target.left; //要删除的是父节点的右节点 然后它有的是左节点
}
}
//2.3.2 右子节点
else
{
//2.3.2.1 要删除的节点是父节点的左节点
if(parent.left.value==value)
{
parent.left=target.right; //要删除的是父节点的右节点 然后它有的是左节点
}
//2.3.2.2 要删除的节点是父节点的右节点
else
{
parent.right=target.right; //要删除的是父节点的右节点 然后它有的是右节点
}
}
}
}
}
//删除右边最小的节点并且获取该节点的值
private int deleteMin(Node node) {
Node target=node;
//递归一直找最左边
while(target.left!=null){ //右边的子树里面的左节点一直可以找下去 就一定是最小的
target=target.left;
}
//最小的值有右子节点
delete(target.value); //那么剩下了一个叶子节点肯定会通过delete方法补上去
return target.value; //直接返回结果
}
//查找父节点
public Node searchParent(int value){
if(root==null){
return null;
}else{
return root.searchParent(value);
}
}
}
|
Node类写具体实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
| package com.company.erchapaixushu;
public class Node {
int value; //此节点的值
Node left; //左节点
Node right; //右节点
public Node(int value){
this.value=value; //构造方法获取值
}
//向子树中添加节点
public void add(Node node) {
//1.传入的节点为空
if(node==null){
return; //直接结束
}
//2.传入的节点的值和当前子树的根节点大小关系
//2.1 传入节点值 < 子树的根节点的值
if(node.value<this.value) {
//2.1.1 当前子树的根节点下面没有左子树 -- 直接添加
if(this.left==null){
this.left=node; //直接添加到左节点
//2.1.2 当前子树的根节点下面有左子树 -- 需要递归去找到
}else{
this.left.add(node); // 在当前子树的根节点下面的左节点下面去添加 (递归)
}
}
//2.2 传入节点值 > 子树的根节点的值
else{
//2.1.1 当前子树的根节点下面没有左子树 -- 直接添加
if(this.right==null){
this.right=node; //直接添加到左节点
//2.1.2 当前子树的根节点下面有左子树 -- 需要递归去找到
}else{
this.right.add(node); // 在当前子树的根节点下面的左节点下面去添加 (递归)
}
}
}
//中序遍历(刚好是从小到大)
public void midShow(Node node) {
if(node==null){
return; //为空就结束
}
midShow(node.left); //左子树继续递归查
System.out.println(node.value); //打印当前节点的值
midShow(node.right); //右子树继续递归查
}
//查找节点
public Node search(int value) {
//1. 传入的值 == 当前节点值
if(this.value==value){
return this; //返回当前节点
}
//2. 传入的值 < 当前节点值 -- 找左边
else if(value<this.value){
if(left==null){return null;} //为空返回null
return this.left.search(value);
}
//3. 传入的值 > 当前节点值 -- 找右边
else{
if(right==null){return null;} //为空返回null
return this.right.search(value);
}
}
//查找父节点
public Node searchParent(int value) {
if((this.left!=null&&this.left.value==value)||(this.right!=null&&this.right.value==value)){
return this; //它的左子节点或者右子节点符合条件
}else {
if(this.value>value&&this.left!=null){
return this.left.searchParent(value); //左边
}else
if(this.value<value&&this.right!=null){
return this.right.searchParent(value); //右边
}
}
return null; //都不满足 返回空
}
}
|
TestBinarySortTree类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| package com.company.erchapaixushu;
public class TestBinarySortTree {
public static void main(String[] args) {
int[] arr=new int[]{7,3,10,12,5,1,9};
//1. 创建一颗二叉排序树
BinarySortTree bst=new BinarySortTree();
//2. 循环添加
for(int i:arr){
bst.add(new Node(i));
}
//3. 中序遍历
bst.midShow();
System.out.println("----------------------");
//4. 查找数中的值
Node node = bst.search(10);
System.out.println("查找值为10的节点的值 : "+node.value);
Node node2 = bst.search(20);
System.out.println("查找值为20的节点是不是为空 : "+node2);
System.out.println("----------------------");
//5. 查看父节点
Node p1=bst.searchParent(10);
System.out.println("输入的值的父节点是: "+p1.value);
System.out.println("----------------------");
//6. 删除叶子节点
bst.delete(5); //删除叶子节点
bst.midShow(); //删除之后查看
System.out.println("----------------------");
//7. 删除有一个节点的节点
bst.delete(3); //有一个1的左节点
bst.midShow();
System.out.println("----------------------");
//8. 删除有两个子节点
bst.delete(7); //根节点
bst.midShow();
System.out.println("----------------------");
}
}
|
结果展示
叶子节点和有一个节点的值:

有两个节点的值:

平衡二叉树(AVL树)
平衡二叉树概念
前提: 必须是一个二叉排序树
条件: 任何一个非叶子节点满足: |左子树高度-右子树高度|<1
存在意义: 提高一般的二叉排序树的查找效率
准备获高度方法和add方法添加判断平衡
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| 之前的add方法内部需要判断是不是平衡!!!!!!!
//3. 查询是否平衡
//3.1 左左情况(向右转)
if(leftHight()-rightHight()>=2) //左边太多 向右转(原来根的左节点作为新的根节点)
{
rightRotate(); //调用具体实现内写的方法
}
//3.2 右右情况(向左转)
if(leftHight()-rightHight()<=-2) //右边太多 向左转(原来根的右节点作为新的根节点)
{
leftRotate(); //调用具体实现内写的方法
}
-------------------------------
//当前节点的高度
public int height(){
return Math.max(left==null?0:left.height(),right==null?0:right.height())+1; //当前节点高度=左右子树最大的+1
}
//左子树的高度 (避免为空)
public int leftHight(){
if(left==null){ //有可能为空
return 0;
}
return left.height();
}
//右子树的高度 (避免为空)
public int rightHight(){
if(right==null){ //有可能为空
return 0;
}
return right.height();
}
|
构造平衡二叉树(单旋转)
左左情况(右旋转)
左左情况怎么变换:
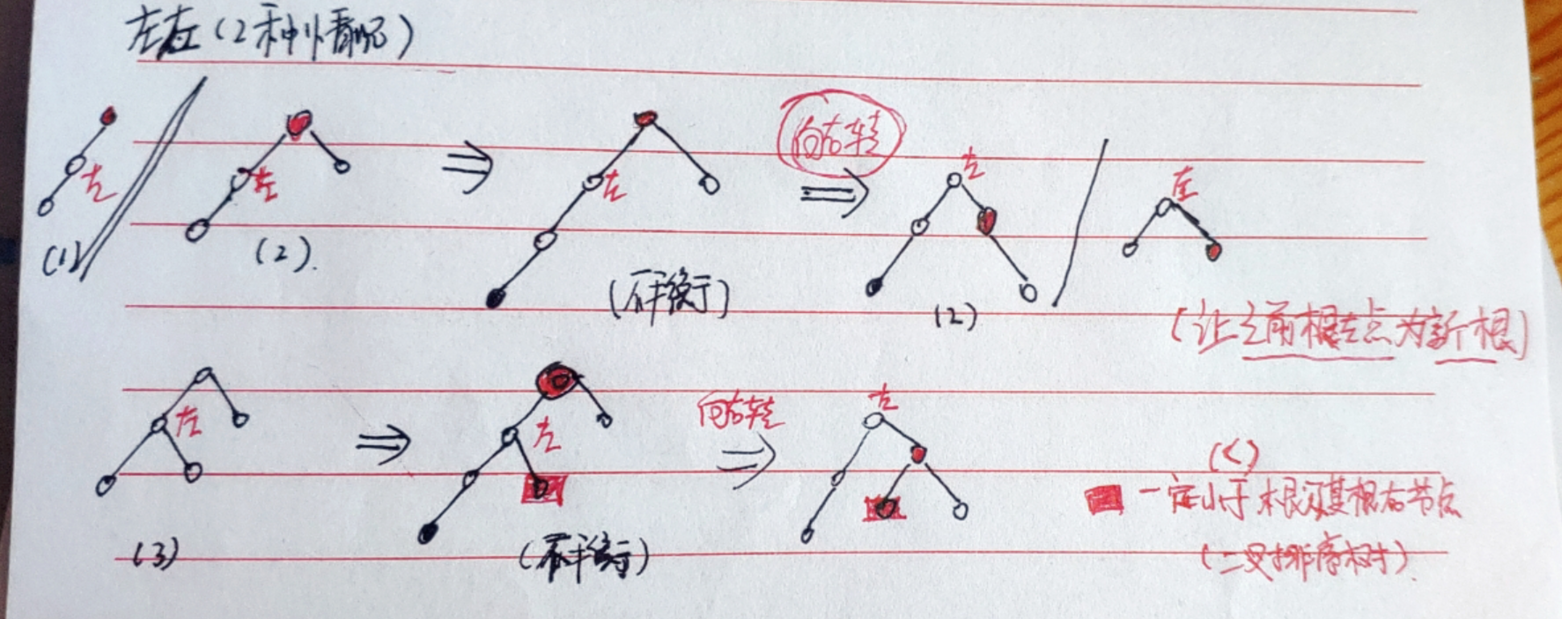
左左情况代码实现:
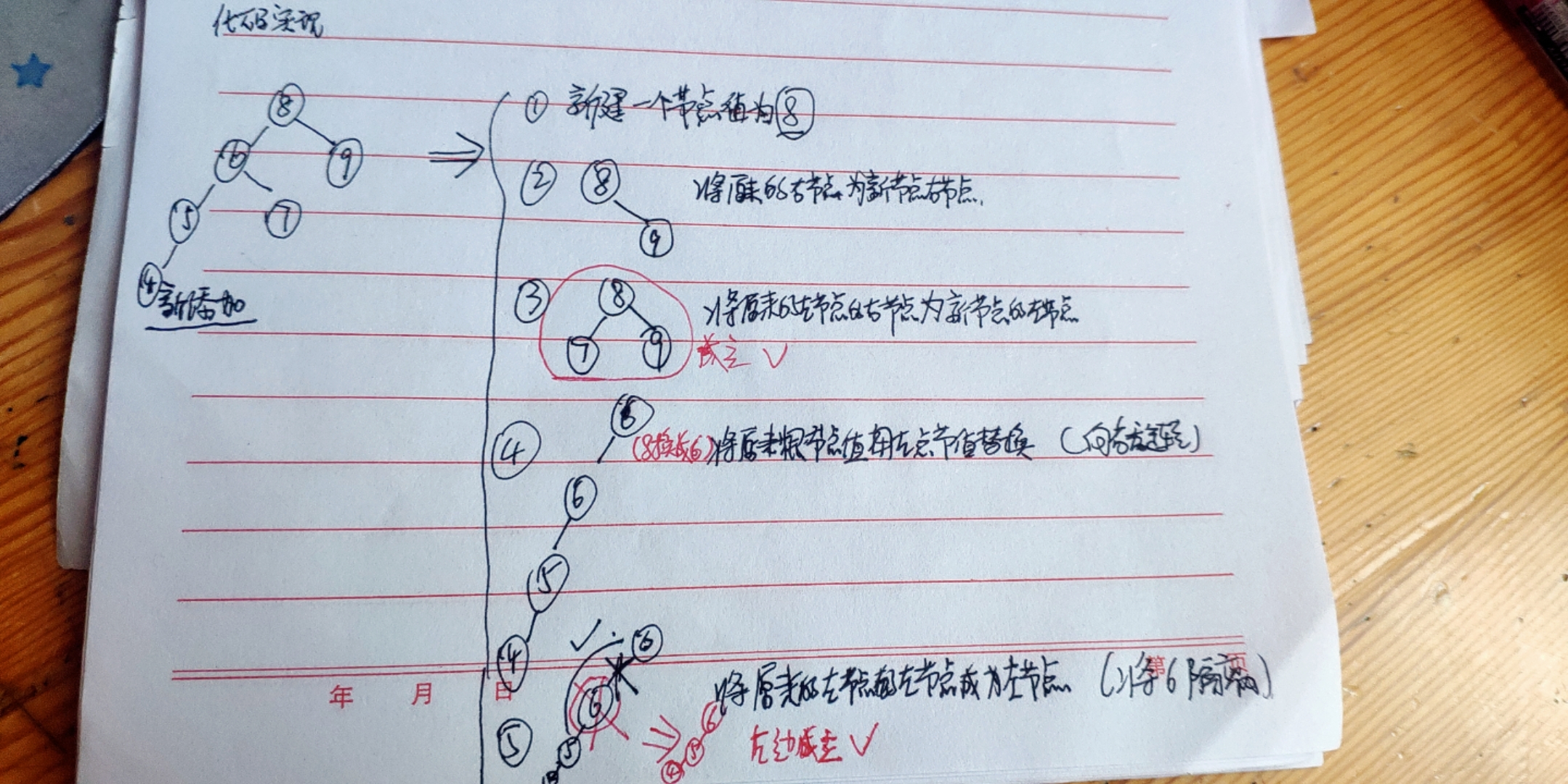
Node类实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| //左左情况 -- 右旋转
private void rightRotate() {
//1. 创建新节点(值==当前节点的值)
Node newRight=new Node(this.value);
//2. 当前节点的右节点 --> 新节点的右节点 (原来的根节点和它右边子树已经挪走了)
newRight.right=this.right;
//3. 当前节点的左节点的右节点 --> 新节点的左节点 (原来的根节点的左节点的右子树成为新节点的左节点)
newRight.left=this.left.right;
//4. 当前节点值 --> 当前节点的左节点的值 (左边节点被替换掉)
this.value=this.left.value;
//5. 当前节点的左节点的左节点 --> 当前节点的左节点 (相当于直接把当前节点的左节点被扔出去)
this.left=this.left.left;
//6. 新节点 --> 当前节点的右节点
this.right=newRight;
}
|
右右情况(左旋转)
右右情况怎么变换:
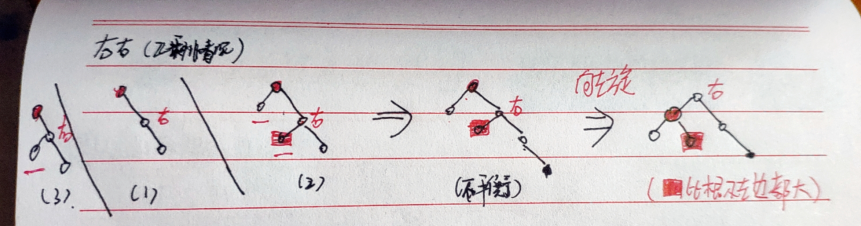
右右情况代码实现:
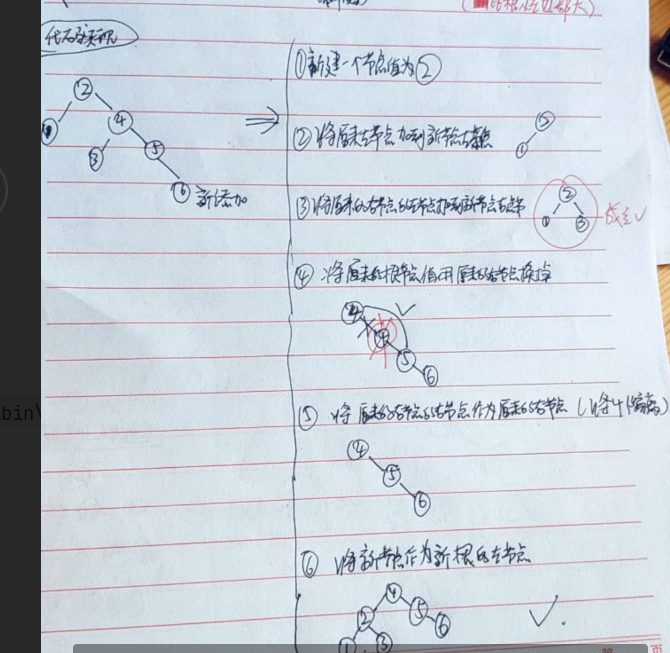
Node类实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| //右右情况 -- 左旋转
private void leftRotate() {
//1. 创建新节点(值==当前节点的值)
Node newLeft=new Node(this.value);
//2. 当前节点的左节点 --> 新节点的左节点 (原来的根节点和它左边子树已经挪走了)
newLeft.left=this.left;
//3. 当前节点的右节点的左节点 --> 新节点的右节点 (原来的根节点的右节点的左子树成为新节点的右节点)
newLeft.right=this.right.left;
//4. 当前节点值 --> 当前节点的右节点的值 (右边节点被替换掉)
this.value=this.right.value;
//5. 当前节点的右节点的右节点 --> 当前节点的右节点 (相当于直接把当前节点的右节点被扔出去)
this.right=this.right.right;
//6. 新节点 --> 当前节点的左节点
this.left=newLeft;
}
|
完整代码
Node类(二叉排序树的基础上添加 查询高度的方法 + 左/右旋转的方法 + add方法判断是否平衡)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
| public class Node {
int value; //此节点的值
Node left; //左节点
Node right; //右节点
public Node(int value){
this.value=value; //构造方法获取值
}
//向子树中添加节点
public void add(Node node) {
//1.传入的节点为空
if(node==null){
return; //直接结束
}
//2.传入的节点的值和当前子树的根节点大小关系
//2.1 传入节点值 < 子树的根节点的值
if(node.value<this.value) {
//2.1.1 当前子树的根节点下面没有左子树 -- 直接添加
if(this.left==null){
this.left=node; //直接添加到左节点
//2.1.2 当前子树的根节点下面有左子树 -- 需要递归去找到
}else{
this.left.add(node); // 在当前子树的根节点下面的左节点下面去添加 (递归)
}
}
//2.2 传入节点值 > 子树的根节点的值
else{
//2.1.1 当前子树的根节点下面没有左子树 -- 直接添加
if(this.right==null){
this.right=node; //直接添加到左节点
//2.1.2 当前子树的根节点下面有左子树 -- 需要递归去找到
}else{
this.right.add(node); // 在当前子树的根节点下面的左节点下面去添加 (递归)
}
}
//3. 查询是否平衡
//3.1 左左情况(向右转)
if(leftHight()-rightHight()>=2){ //左边太多 向右转(原来根的左节点作为新的根节点)
rightRotate();
}
//3.2 右右情况(向左转)
if(leftHight()-rightHight()<=-2) {
leftRotate();
}
}
//右右情况 -- 左旋转
private void leftRotate() {
//1. 创建新节点(值==当前节点的值)
Node newLeft=new Node(this.value);
//2. 当前节点的左节点 --> 新节点的左节点 (原来的根节点和它左边子树已经挪走了)
newLeft.left=this.left;
//3. 当前节点的右节点的左节点 --> 新节点的右节点 (原来的根节点的右节点的左子树成为新节点的右节点)
newLeft.right=this.right.left;
//4. 当前节点值 --> 当前节点的右节点的值 (右边节点被替换掉)
this.value=this.right.value;
//5. 当前节点的右节点的右节点 --> 当前节点的右节点 (相当于直接把当前节点的右节点被扔出去)
this.right=this.right.right;
//6. 新节点 --> 当前节点的左节点
this.left=newLeft;
}
//左左情况 -- 右旋转
private void rightRotate() {
//1. 创建新节点(值==当前节点的值)
Node newRight=new Node(this.value);
//2. 当前节点的右节点 --> 新节点的右节点 (原来的根节点和它右边子树已经挪走了)
newRight.right=this.right;
//3. 当前节点的左节点的右节点 --> 新节点的左节点 (原来的根节点的左节点的右子树成为新节点的左节点)
newRight.left=this.left.right;
//4. 当前节点值 --> 当前节点的左节点的值 (左边节点被替换掉)
this.value=this.left.value;
//5. 当前节点的左节点的左节点 --> 当前节点的左节点 (相当于直接把当前节点的左节点被扔出去)
this.left=this.left.left;
//6. 新节点 --> 当前节点的右节点
this.right=newRight;
}
//当前节点的高度
public int height(){
return Math.max(left==null?0:left.height(),right==null?0:right.height())+1; //当前节点高度=左右子树最大的+1
}
//左子树的高度 (避免为空)
public int leftHight(){
if(left==null){ //有可能为空
return 0;
}
return left.height();
}
//右子树的高度 (避免为空)
public int rightHight(){
if(right==null){ //有可能为空
return 0;
}
return right.height();
}
//中序遍历(刚好是从小到大)
public void midShow(Node node) {
if(node==null){
return; //为空就结束
}
midShow(node.left); //左子树继续递归查
System.out.println(node.value); //打印当前节点的值
midShow(node.right); //右子树继续递归查
}
//查找节点
public Node search(int value) {
//1. 传入的值 == 当前节点值
if(this.value==value){
return this; //返回当前节点
}
//2. 传入的值 < 当前节点值 -- 找左边
else if(value<this.value){
if(left==null){return null;} //为空返回null
return this.left.search(value);
}
//3. 传入的值 > 当前节点值 -- 找右边
else{
if(right==null){return null;} //为空返回null
return this.right.search(value);
}
}
//查找父节点
public Node searchParent(int value) {
if((this.left!=null&&this.left.value==value)||(this.right!=null&&this.right.value==value)){
return this;
}else {
if(this.value>value&&this.left!=null){
return this.left.searchParent(value);
}else
if(this.value<value&&this.right!=null){
return this.right.searchParent(value);
}
}
return null;
}
}
|
** TestBinarySortTree类(尝试输出)**
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public class TestBinarySortTree {
public static void main(String[] args) {
int[] arr=new int[]{8,9,6,7,5,4}; //用于改变左边不平衡
//int[] arr=new int[]{2,1,4,3,5,6}; //用于改变右边不平衡
//1. 创建一颗二叉排序树
BinarySortTree bst=new BinarySortTree();
//2. 循环添加
for(int i:arr){
bst.add(new Node(i));
}
//3.查看高度
System.out.println("左左情况变为平衡二叉树之后树的高度:"+bst.root.height());
//4.查看根节点的值(更新后的)
System.out.println("左左情况变为平衡二叉树之后根的值"+bst.root.value);
//5.中序遍历
System.out.println("中序遍历左左情况之后:");
bst.midShow();
}
}
|
BinarySortTree类(和之前的二叉排序树没有变化)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
| public class BinarySortTree {
//root根节点
Node root;
//向二叉排序树中添加节点
public void add(Node node){
//1. 如果是空树
if(root==null){
root=node; //这个节点添加为根节点
}
//2. 不是空树
else{
root.add(node); //调用Node类的方法添加
}
}
//中序遍历(刚好是从小到大)
public void midShow(){
if(root!=null){
root.midShow(root); //查找这个根节点开始的中序遍历
}
}
//查找节点
public Node search(int value){
//1. 如果空树 -- 返回null
if(root==null){
return null;
}
//2. 如果不为空
else{
return root.search(value);
}
}
//删除节点
public void delete(int value){
if(root==null)
{
return; //空树直接返回
}
else
{
//1. 找到这个节点
Node target = search(value);
if(target==null)
{
return;
}
//2. 找到它的父节点
Node parent=searchParent(value);
//2.1 要删除的是叶子节点
if(target.left==null&&target.right==null)
{
//2.1.1 要删除的节点是父节点的左节点
if (parent.left.value == value)
{
parent.left = null; //直接让父节点把它为null
}
//2.1.2 要删除的节点是父节点的右节点
else
{
parent.right = null; //直接让父节点把它为null
}
}
//2.2 要删除的节点有两个子节点
else
if(target.left!=null&&target.right!=null)
{
//2.2.1 删除右子树最小的节点并且获取到该节点的值
int min=deleteMin(target.right);
//2.2.2 替换目标节点中的值
target.value=min;
}
//2.3 要删除的节点是有一个子节点
else
{
//2.3.1 左子节点
if(target.left!=null)
{
//2.3.1.1 要删除的节点是父节点的左节点
if(parent.left.value==value)
{
parent.left=target.left; //要删除的是父节点的左节点 然后它有的是左节点
}
//2.3.1.2 要删除的节点是父节点的右节点
else
{
parent.right=target.left; //要删除的是父节点的右节点 然后它有的是左节点
}
}
//2.3.2 右子节点
else
{
//2.3.2.1 要删除的节点是父节点的左节点
if(parent.left.value==value)
{
parent.left=target.right; //要删除的是父节点的右节点 然后它有的是左节点
}
//2.3.2.2 要删除的节点是父节点的右节点
else
{
parent.right=target.right; //要删除的是父节点的右节点 然后它有的是右节点
}
}
}
}
}
//删除右边最小的节点并且获取该节点的值
private int deleteMin(Node node) {
Node target=node;
//递归一直找最左边
while(target.left!=null){ //右边的子树里面的左节点一直可以找下去 就一定是最小的
target=target.left;
}
//最小的值有右子节点
delete(target.value); //那么剩下了一个叶子节点肯定会通过delete方法补上去
return target.value; //直接返回结果
}
//查找父节点
public Node searchParent(int value){
if(root==null){
return null;
}else{
return root.searchParent(value);
}
}
}
|
测试左左情况结果:

测试右右情况结果:
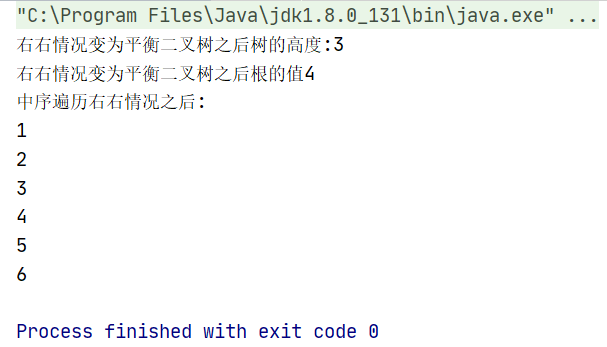
构造平衡二叉树(双旋转)
二叉排序树经过一次旋转之后还是不平衡的所以还需要第二次旋转
双旋转条件
1. 根的左节点的左高度 < 右高度(左少右多) -- 1.1 根的左节点先左旋转 1.2 整体再右旋转
2. 根的右节点的右高度 < 左高度(左多右少) -- 2.1 根的右节点先右旋转 2.2 整体再左旋转
举例:
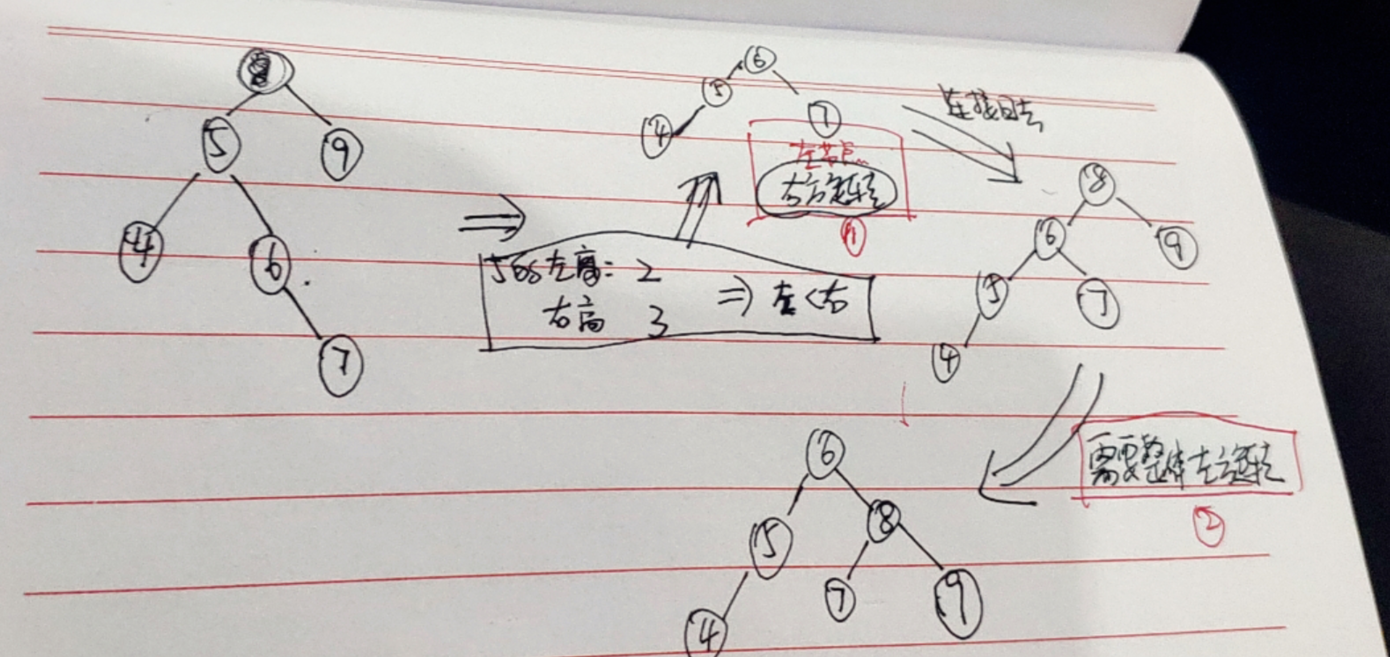
Node类更新(单循环添加特定条件)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| //3.1 左左情况(向右转)
if(leftHight()-rightHight()>=2){ //左边太多 向右转(原来根的左节点作为新的根节点)
//3.1.1 双旋转
if(left!=null&&left.leftHight()<left.rightHight()){ //根的左节点的左高度<右高度
left.leftRotate(); //左节点先左旋转
rightRotate(); //整体再右旋转
}
//3.1.2 单旋转
else{
rightRotate();
}
}
//3.2 右右情况(向左转)
if(leftHight()-rightHight()<=-2) {
//3.2.1 双旋转
if(right!=null&&right.rightHight()<right.leftHight()){ //根的右节点的右高度<左高度
right.rightRotate(); //右节点先右旋转
leftRotate(); //整体再左旋转
}
//3.2.2 单旋转
else {
leftRotate();
}
|
双旋转结果:

多路查找树
多路查找树分类:
1. 2-3树(B树的特例)
2. 2-3-4树(B树的特例)
3. B树和B+树
数据存储原理
B树提高普通二叉树的效率:
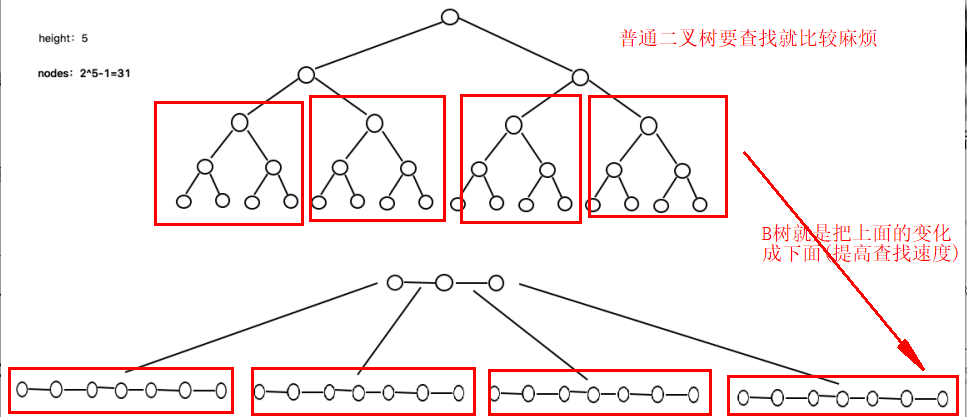
2-3树原理
满足条件:
1. B树中所有的叶子节点都在同一层
2. 有两个子节点的节点 --> 二节点 (二节点要么有两个节点,要么没有子节点)
3. 有三个子节点的节点 --> 三节点 (三节点要么有三个节点,要么没有子节点)
4. 有四个子节点的节点 --> 四节点 (四节点要么有四个节点,要么没有子节点)
B树和B+树原理
很多的二/三/四节点组成的二叉树
B树和B+树的区别
1. B+树的叶子节点存放内容(有序的链式结构)






















