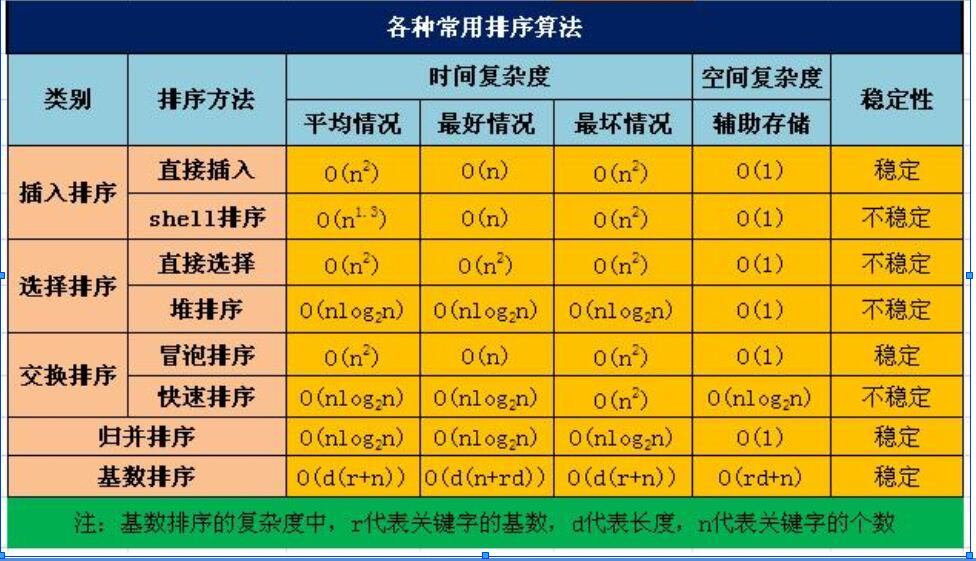
排序算法(8个) 排序算法概述:
性能对比:
冒泡排序 原理 1.比较两个相邻的元素,将值大的元素交换到右边(直到比较最后两个数)
2.然后开始下一轮,直至倒数第二个数交换成功动态图:
具体实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public class BubbleSort { public static void main(String[] args){ int []arr=new int[]{5,7,2,9,4,1,0,5,7}; System.out.println(Arrays.toString(arr)); //先输出之前的数组 maopao(arr) ; System.out.println(Arrays.toString(arr)); //输出排序之后的数组 } //冒泡排序 public static void maopao(int[] arr){ //控制共比较多少轮(除过最后一个数都需要去排序) for(int i=0;i<arr.length-1;i++){ //控制比较次数(每次排序时之前拍好的数字就不需要比较) for(int j=0;j<arr.length-1-i;j++){ if(arr[j]>arr[j+1]){ int temp=arr[j]; //三个数交换的方法 arr[j]=arr[j+1]; arr[j+1]=temp; } } } } }
结果:
快速排序 原理 1. 选择一个标准数(随机数/第一个) --> 一列数字分为左小右大
2. 确定左右两个指针low和high(low<high的情况下去将判断的数字区分成两类数)
3. 确定start和end两个数为数组的一开始和一结束(start<end的情况下快速排序还没有结束)
4. 判断指针左移和数字交换 (假设标准数为2)
4.1 判断最右边开始的数字
4.1.1 如果标准数比最右边的数小 2<=9 high指针左移 2 9
4.1.2 如果标准数比最右边的数大 2>=1 用1把2替换掉 1 2 (一旦换数字就判断左边的去)
4.2 接下来判断最左边开始的数字
4.2.1 如果最左边的数比标准数小 1<=2 low指针右移 1 2
4.2.2 如果最左边的数比标准数大 3>=2 用2把3替换掉 2 3 (一旦换数字就判断右边的去)
4.3 不断地判断右边的只要换数字了就判断左边的只要换数字就继续交替执行!!!!!!!!!!!
5. 因为low和high碰在 要把重复的值用标准值去替换掉(low和high指向的同一个位置的那个数字要么替换了右边的要么被右边替换过来的所以肯定是两个重复的数字需要用标准值替换)
6. 接下来就是递归调用方法(不断地让两边去快排)
6.1 处理左边的数字
kuaisu(arr,start,low) //从start到low指针
6.2 处理右边的数字
kuaisu(arr,low+1,end) //从low+1的位置到end 动态图:
分析图示:
具体实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 public class QuickSort { public static void main(String[] args) { int []arr=new int[]{5,7,2,9,4,1,0,5,7}; System.out.println(Arrays.toString(arr)); //输出之前的数组 kuaisu(arr,0,arr.length-1); //开头和结尾相当于指针 System.out.println(Arrays.toString(arr)); //输出排序之后的数组 } public static void kuaisu(int[] arr,int start,int end){ //传入数组和前后两个参数 if(start<end){ //如果左边和右边冲突就是快速排序的结束条件 //将第一个数作为标准数 int biao=arr[start]; //需要排序的下标 int low=start; int high=end; //找比标准大的数字和比标准小的数字 while(low<high){ while(low<high&&biao<=arr[high]){ // 假设标准数是2 <= 右边现在数是9 high--; //右边的指针左移(符合条件) } //使用右边的数字替换左边的数字 (标准数是2 >= 右边是1 ) arr[low]=arr[high]; //用1把2替换掉(做到小数左移) //如果左边的数字比标准数小 while(low<high&&arr[low]<=biao){ low++; //左边指针右移(符合条件) } //使用左边的数字替换右边的数字 ( 左边的8 >= 标准数是2) arr[high]=arr[low]; //将8替换2 } //标准数替换掉重复的数字(low/high都可以) arr[low]=biao; //处理所有小的数字 kuaisu(arr,start,low); //处理所有大的数字 kuaisu(arr,low+1,end); } } }
结果:
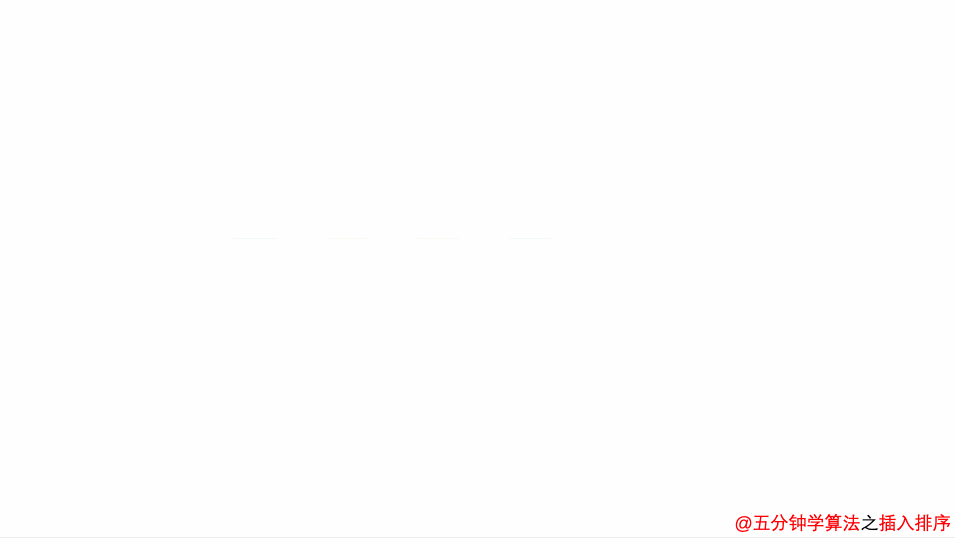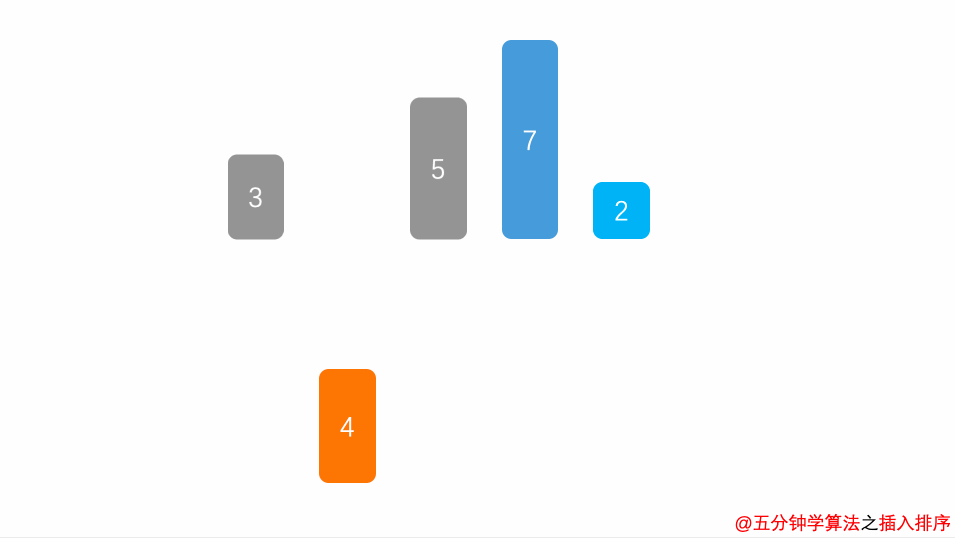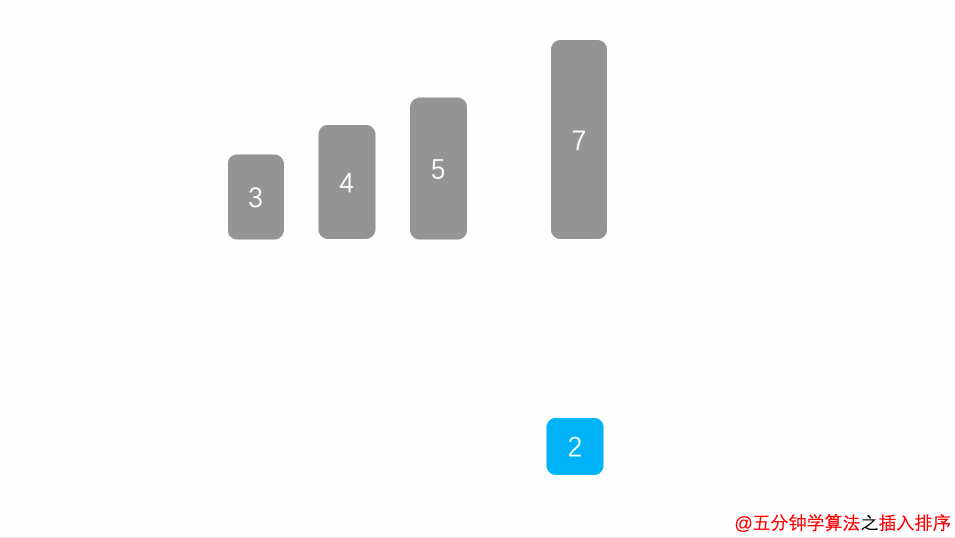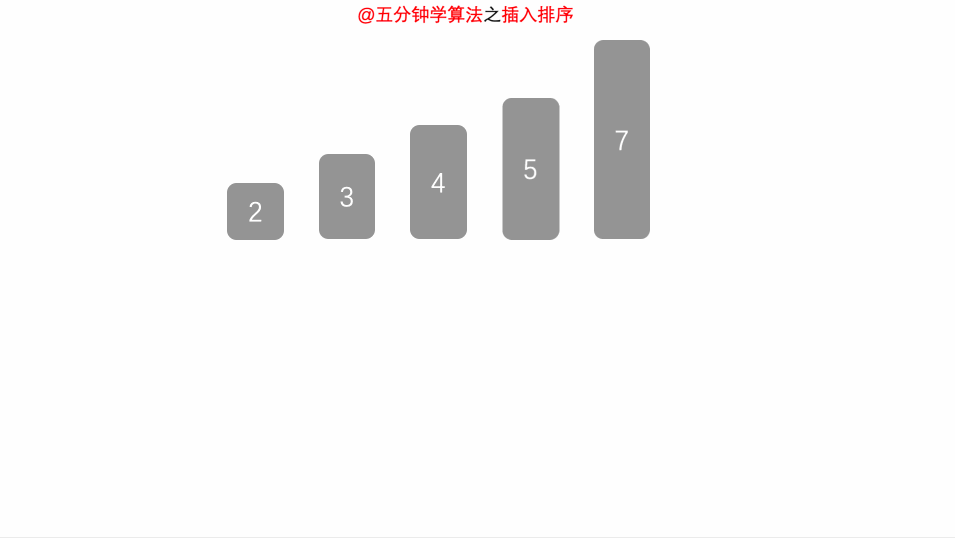
插入排序(直接插入排序) 原理 1. 最大的特点就是:我在排当前数的时候前面的数必须是有序的
2. 从第二个数开始
2.1 遍历所有前面的数字 如果当前数(2) < 前面的数字(3 4) : 说明我还可以左移 (前面的数字给后面的数字)
2.2 如果当前数(2) > / = 前面的数(1 2 3) : 说明已经不用挪动了就可以2替换3的位置 (3已经在上面的条件里面挪到后面了)动态图:
具体实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public class Main { public static void main(String[] args) { Scanner input = new Scanner(System.in); //int n=input.nextInt(); int[] a=new int[]{1,5,3,6,9,4,11,87,23}; find(a); //调用方法返回结果 System.out.println(Arrays.toString(a)); } public static void find(int[] a){ for(int i=1;i<a.length;i++){ //从第二位开始遍历 int temp=a[i]; //将要插入的数字存放到temp里面 int flag; //定义flag下标 因为for循环外面还要用 for(flag=i-1;flag>=0&&a[flag]>temp;flag--){ //找0到i-1位置遍历 a[flag+1]=a[flag]; //只有满足前面比要插入的数字大 才让他往后挪动 } a[flag+1]=temp; //最后flag通过for会给一个值 然后将要插入的数字插入位置 } } }
结果:
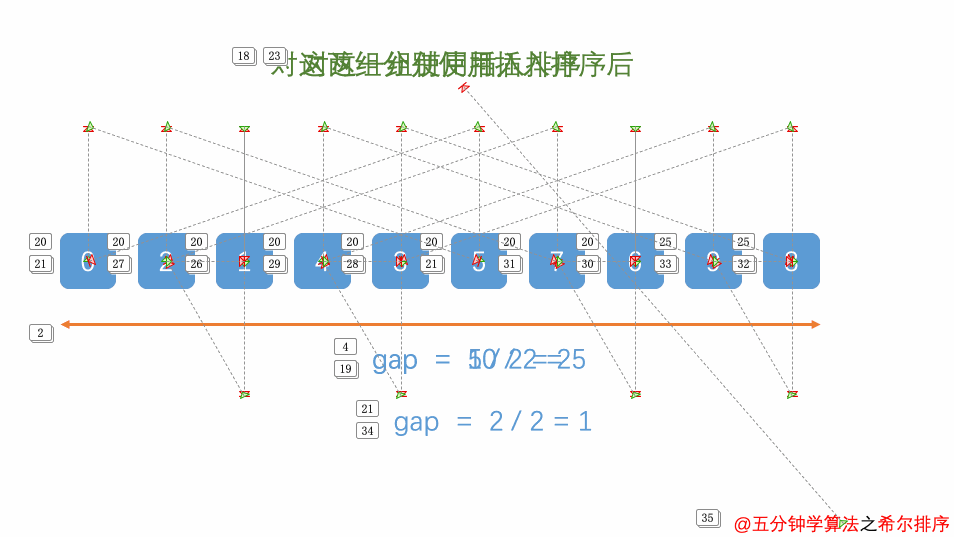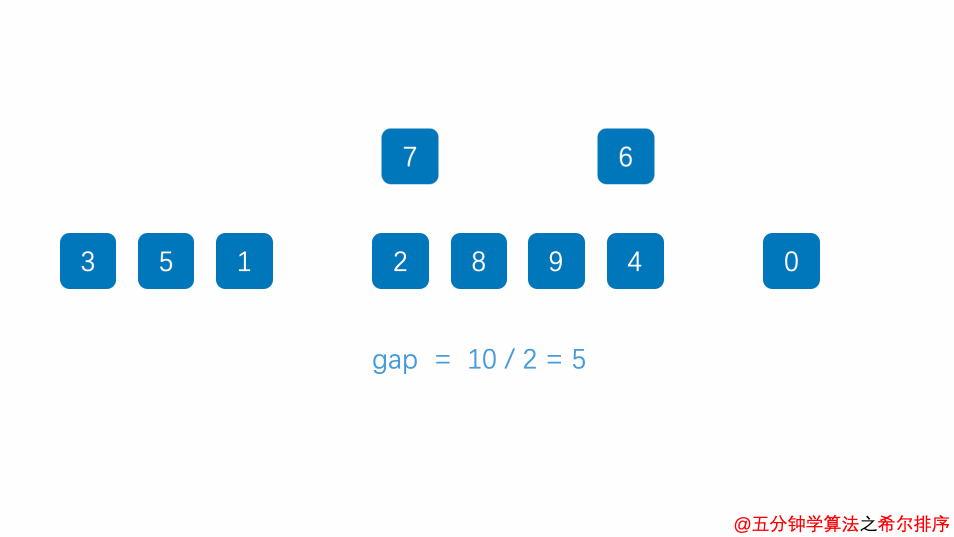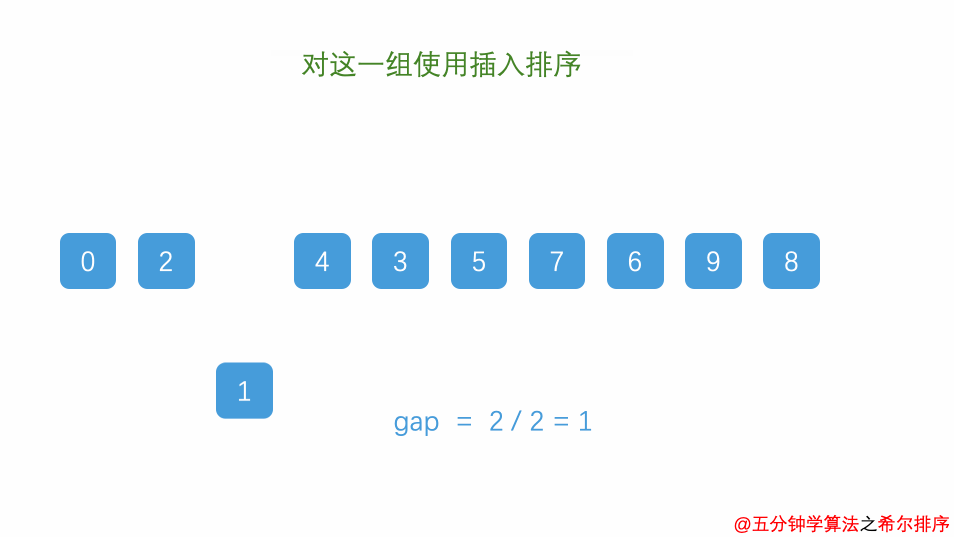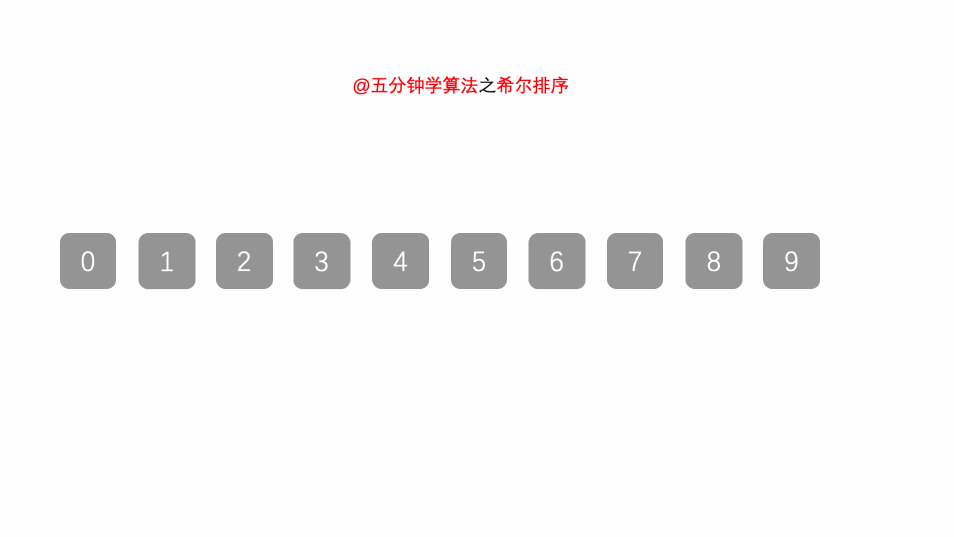
插入排序(希尔排序) 原理 1. 根据(总数/2)的方法不断去组队排序
假如是9个数字 :
1.1 第一轮是9/2=4(按照4的间隔对应的数字排序 0和4和8位置的排序对比 1和5的对比 2和6的对比 3和7的对比)
1.2 第二轮是4/2=2(按照2的间隔对应的数字进行排序对比 )
1.3 直到/2为1的时候结束
2. 通过这个方法比直接插入排序效率高(万一最后一个数字是最小的话就可以很快速的放到前面去)动态图:
具体实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public class ShellSort { public static void main(String[] args) { int []arr=new int[]{5,7,2,9,4,1,0,5,7}; System.out.println(Arrays.toString(arr)); shellSort(arr); System.out.println(Arrays.toString(arr)); } public static void shellSort(int[] arr){ //遍历所有的步长 for(int d=arr.length/2;d>0;d/=2){ //遍历所有的元素 for(int i=d;i<arr.length;i++){ //遍历一个组的所有元素 for(int j=i-d;j>=0;j-=d){ //j是从 if(arr[j]>arr[j+d]){ //前大于后 3 2 int temp=arr[j]; //两个数交换 arr[j]=arr[j+d]; arr[j+d]=temp; } } } } } }
结果:
选择排序(简单选择排序) 原理 1. 我们就是每次都判断之后的所有的数字。每次把最小的数字换到判断的这个点上。
2. 如果后面有比现在的位置小的数字就把下标记下来最后让之前的最小的数字的下标和现在的数字更换位置。具体实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public class XuanZ { public static void main(String[] args) { int[] arr=new int[]{3,4,5,7,1,2,0,3,6,8}; System.out.println(Arrays.toString(arr)); //输出未排序的顺序 xuanze(arr); System.out.println(Arrays.toString(arr)); //排序之后的顺序 } public static void xuanze(int[] arr) { //遍历所有的数 for(int i=0;i<arr.length;i++){ int minIndex=i; //把当前遍历的数和后面所有的数依次进行比较 //记录最小的数的下标 for(int j=i+1;j<arr.length;j++){ //从第二个开始 if(arr[minIndex]>arr[j]){ //后面有数字更小 就把它记录下 minIndex=j; } } //最小的数和当前遍历的下标不一致 后面有数字替换了当前的数字 if(i!=minIndex){ int temp=arr[i]; arr[i]=arr[minIndex]; arr[minIndex]=temp; } } } }
结果:
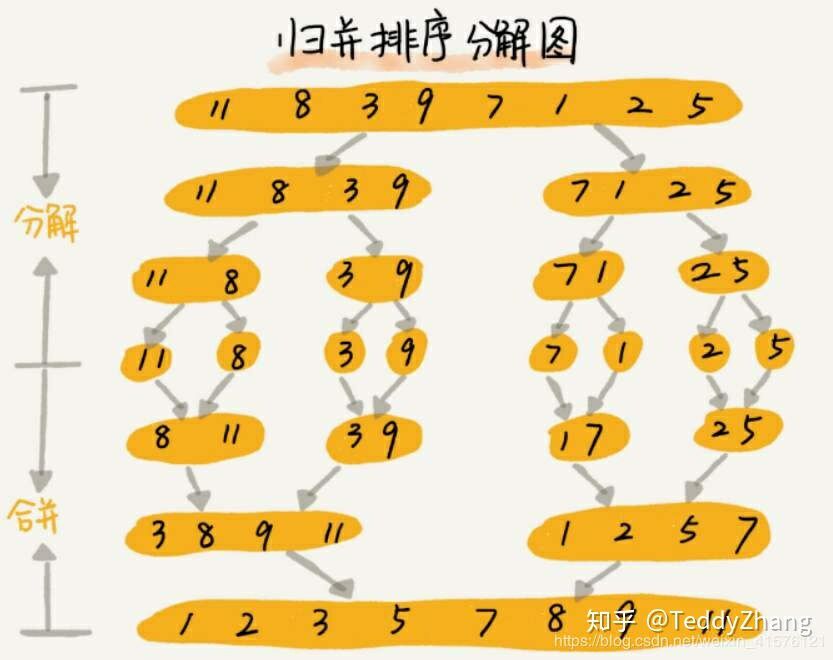
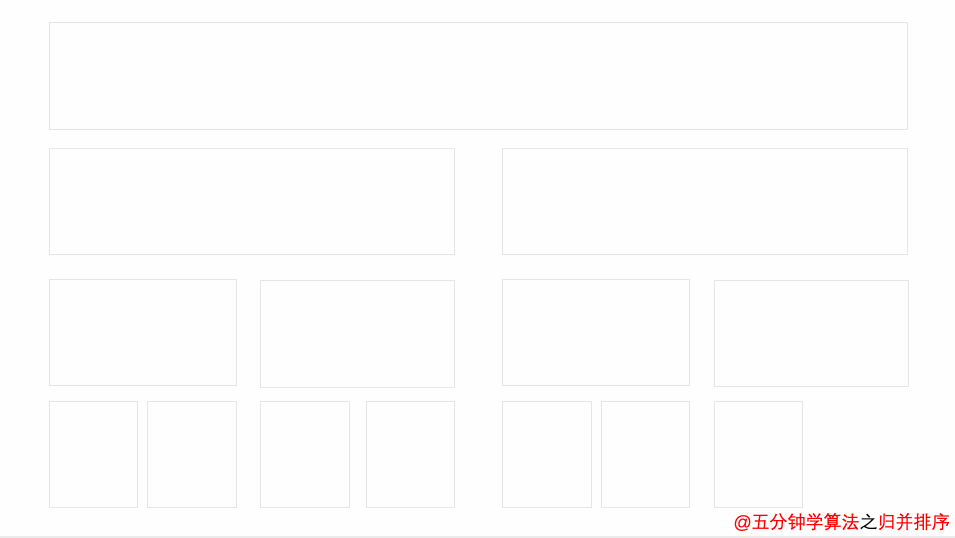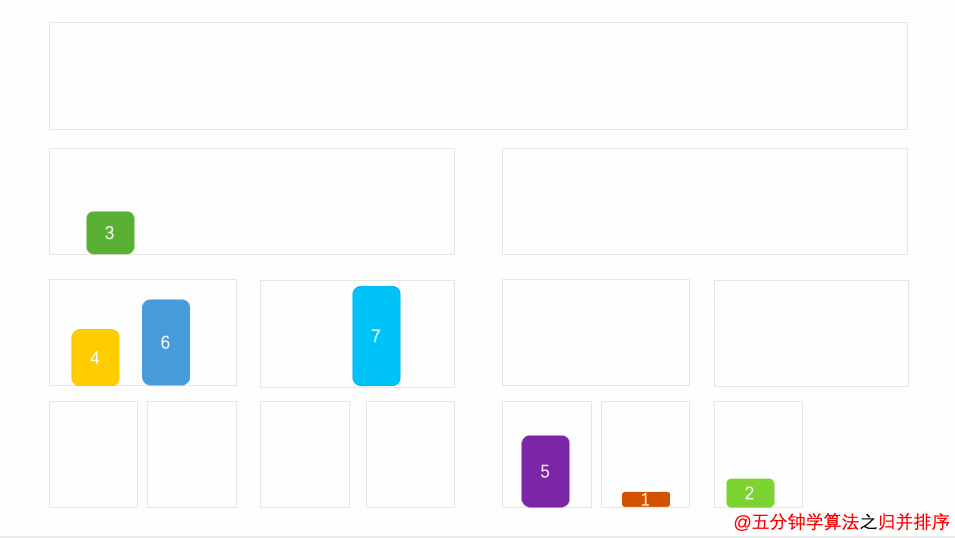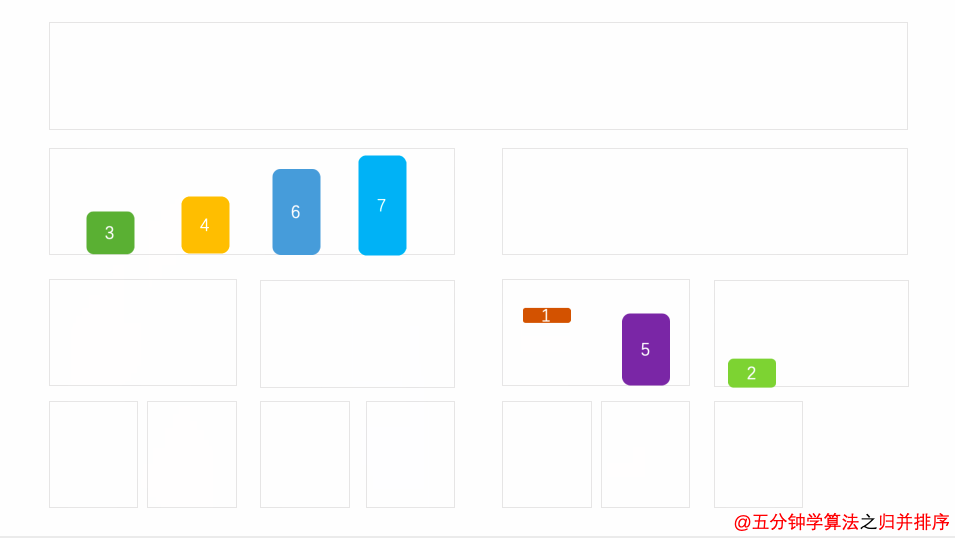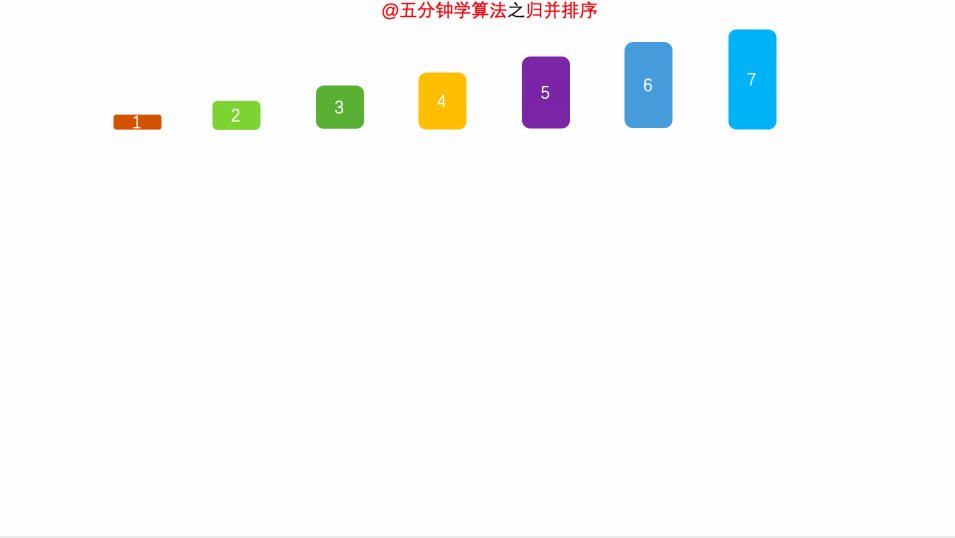
归并排序(递归) 原理 1. 将其划分为两部分一直到不能分解(递归)
2. 两部分开始归并
3. 最终返回回来就是一个排序好的数组 递归思路:
动态图:
具体实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 public class GuiB { public static void main(String[] args) { int[] arr=new int[]{1,3,5,2,4,6,8,10}; System.out.println(Arrays.toString(arr)); //排序前 mergeSort(arr,0,arr.length-1); System.out.println(Arrays.toString(arr)); //排序后 } public static void mergeSort(int[] arr,int low,int high){ int middle=(high+low)/2; //取中间位置 if(low<high) { mergeSort(arr,low,middle); //处理左边 mergeSort(arr,middle+1,high); //处理右边 merge(arr,low,middle,high); //归并 } } public static void merge(int[]arr,int low,int middle,int high){ //用于存储归并后的临时数组 int[] temp=new int[high-low+1]; //记录第一个数组中需要遍历的下标 int i=low; //记录第二个数组中需要遍历的下表 int j=middle+1; //记录临时变量存放下标 int index=0; //遍历两个数组 取出小的数字放如临时数组中 while (i<=middle&&j<=high){ if(arr[i]<=arr[j]){ //左边数组的小 放入之后下标++ temp[index]=arr[i]; i++; index++; } else{ //右边数组的小 放入之后下标++ temp[index]=arr[j]; j++; index++; } } //处理多余数据 while(j<=high){ //右边数组多了 temp[index]=arr[j]; j++; index++; } while(i<=middle){ //左边数组多了 temp[index]=arr[i]; i++; index++; } //临时数组重新存入 for(int k=0;k<temp.length;k++){ arr[k+low]=temp[k]; } } }
结果:
基数排序(适用多位数) 原理 1. 大概思路就是每次对排序的数字进行取余(个位到十位一直到最大数字的最高位停止)
2. 每次取余之后把数字放在余数和0..9对应的二维数组内 (第一次是99 取余之后是9就放在二维数组第一个属性是9的位置里面)
3. 然后按照0..9的顺序从二维数组取出来放入原来的数组 然后又取余数按照余数放进二维数组
4. 一直到最后一次取出来就肯定是按顺序动态图:
具体实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 public class RadixSort { public static void main(String[] args) { int[] arr=new int[]{23,6,9,189,45,6,8,123549,56}; //需要排序的数字 jishu(arr); System.out.println(Arrays.toString(arr)); //排序之后 } public static void jishu(int[] arr){ //存储数组中最大的数字 --确定排几次 int max=Integer.MIN_VALUE; for(int i=0;i<arr.length;i++){ if(arr[i]>max){ max=arr[i]; //取出来最大的数字 后面会求出几位数控制循环范围 } } //求最大数字是几位数 int maxLength=(max+"").length(); //数字+""就会成为字符串 //第一个下标就是表示余数的十个可能 第二个就是每个对应下标存放多少个数字 int[][] temp=new int[10][arr.length]; //0..9的二维数组存放对应余数的数字 //记录相应数组中数个数 int[] counts=new int[10]; //记录0..9的二维数组里面存了几个数字 for(int i=0,n=1;i<maxLength;i++,n*=10){ for(int j=0;j<arr.length;j++){ //每个数字每次计算余数 int ys=arr[j]/n%10; //获取余数 temp[ys][counts[ys]]=arr[j]; //counts[ys]是0..9对应下标存放了几个(方便二维数组存放顺序) counts[ys]++; //存放的数字+1 } //循环取数 int index=0; for(int k=0;k<counts.length;k++){ if(counts[k]!=0){ //记录存了几个数字的数组不为空(二维数组里面有数) for(int l=0;l<counts[k];l++){ //遍历二维数组中存的排序的数字 arr[index++]=temp[k][l]; //数字再放到原来数组 } } } //让记录二维数组存数的数组全部清空 (下一次取余计数好用!!!) for(int z=0;z<counts.length;z++){ counts[z]=0; } } } }
结果:
基数排序(队列)
现在使用队列进行存放(队列添加)和每一次存放之后返回(出队) – 减少了二维数组和计数数组的麻烦
队列 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 public class MyQueue { int[] elements; public MyQueue() { elements=new int[0]; } //入队 public void add(int element) { // 创建一个新的数组 int[] newArr = new int[elements.length + 1]; // 把原数组中的元素复制到新数组中 for (int i = 0; i < elements.length; i++) { newArr[i] = elements[i]; } // 把添加的元素放入新数组中 newArr[elements.length] = element; // 使用新数组替换旧数组 elements = newArr; } //出队 public int poll() { //把数组中的第0个元素取出来 int element = elements[0]; //创建一个新的数组 int[] newArr = new int[elements.length-1]; //复制原数组中的元素到新数组中 for(int i=0;i<newArr.length;i++) { newArr[i]=elements[i+1]; } //替换数组 elements=newArr; return element; } //判断队列是否为空 public boolean isEmpty() { return elements.length==0; } }
主要实现类 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public class RqdixQueueSort { public static void main(String[] args) { int[] arr=new int[]{23,6,9,189,45,6,8,123549,56}; jishu(arr); System.out.println(Arrays.toString(arr)); } public static void jishu(int[] arr){ //存储数组中最大的数字 --确定排几次 int max=Integer.MIN_VALUE; for(int i=0;i<arr.length;i++){ if(arr[i]>max){ max=arr[i]; } } //求最大数字是几位数 int maxLength=(max+"").length(); //数字+""就会成为字符串 //临时存放数字的队列(先进先出) MyQueue[] temp=new MyQueue[10]; for(int i=0;i<temp.length;i++){ temp[i]=new MyQueue(); } for(int i=0,n=1;i<maxLength;i++,n*=10){ for(int j=0;j<arr.length;j++){ //每个数字每次计算余数 int ys=arr[j]/n%10; //获取余数 temp[ys].add(arr[j]); //队列添加 } //数字取出来 int index=0; for(int k=0;k<temp.length;k++){ while(!temp[k].isEmpty()){ //记录存了几个数字的数组不为空 arr[index++]=temp[k].poll(); //队列出队 } } } } }
堆排序(堆) 原理 1. 升序 : 小顶堆
2. 降序 : 大顶堆动态图:
具体实现