2019-11-13

第十届蓝桥杯省赛

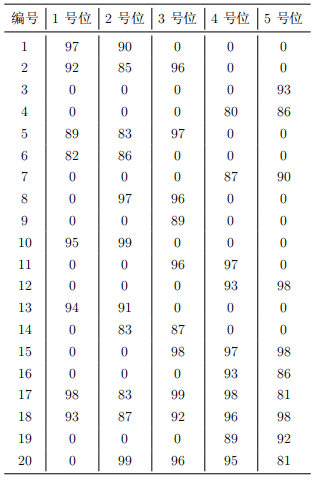
一、组队问题

问题描述
作为篮球队教练，你需要从以下名单中选出 1 号位至 5 号位各一名球员，组成球队的首发阵容。
每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1
号位至 5 号位的评分之和最大可能是多少？

问题分析：
　　这个题目我记得当时我拿到手里没考虑写代码，就是手算的答案490！今天好好考虑了一下这个题目，其实用暴力求解就可以。
　　用一个二维数组来存放这个表的信息，然后设置一些变量来代表1-号位，通过判断条件(五个人必须不一样！！)就可以输出结果。
代码如下：

import java.util.Scanner;
public class Main{
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in); 
		int[][] team = new int[20][5];
		for (int i = 0; i < 20; i++) 
		{
			for (int j = 0; j < 5; j++)
			{
				team[i][j] = input.nextInt();
			}
		}
		
		int maxSum = 0;
		for (int i = 0; i < 20; i++)
			for (int j = 0; j < 20; j++)
				for (int k = 0; k < 20; k++)
					for (int h = 0; h < 20; h++)
						for (int g = 0; g < 20; g++)
							if ((i != j && i != k && i != h && i != g) && (j != k && j != h && j != g)&& (k != h && k != g) && h != g)//必须五个人不同才可以
							{
								int max = team[i][0] + team[j][1] + team[k][2] + team[h][3] + team[g][4];//循环取值计算出每种可能的值
								if (max > maxSum)
									maxSum = max;//输出最大值的可能取值
							}
		System.out.println(maxSum);		
	}
}

代码结果如下：
输出：490

二、不同子串

问题描述
一个字符串的非空子串是指字符串中长度至少为 1 的连续的一段字符组成的串。例如，字符串aaab 有非空子串a, b, aa, ab, aaa, aab, aaab，一共 7 个。注意在计算时，只算本质不同的串的个数。
请问，字符串0100110001010001 有多少个不同的非空子串？
问题分析：
　我记得当时都没算出来，一遇到这种题目我就死了，学完了JAVA的Set集合之后发现可以直接调用其中的方法快速解题！(substring(int i,int j))
代码如下：

import java.util.Scanner;
import java.util.Set;
import java.util.TreeSet;
public class Main{
	public static void main(String[] args) {
		Scanner input=new Scanner(System.in);
	      String s=input.nextLine();
	      Set<String> set=new TreeSet<String>();
	      for (int i = 1; i <= s.length(); ++i) 
	      {// 长度
				for (int j = 0; j <= s.length() - i; ++j)
				{// 起点
					if (!set.contains(s.substring(j, j + i)))
						set.add(s.substring(j, j + i));//增加个数
				}
		}
     	System.out.println(set.size());//输出add之后的长度
  }
}

代码结果如下：

三、数列求值

问题描述
给定数列 1, 1, 1, 3, 5, 9, 17, …，从第 4 项开始，每项都是前 3 项的和。求
第 20190324 项的最后 4 位数字。
问题分析：
　　首先想到的就是用递归求解，但是考虑会超时和内存过大，所以考虑使用动态规划/循环求解；接下来考虑求后四位的话我们不用考虑前面的数字，所以每次求解出来答案就对其与10000取余得出答案。
循环求解：

package javaapplication1;
import java.util.Scanner;
public class JavaApplication1 {
    public static void main(String[] args) {
      Scanner input=new Scanner(System.in);
      int n=input.nextInt();
      int[] a=new int[n];//用数组去存放这个结果
      a[0]=1;
      a[1]=1;
      a[2]=1;//给前三个数字赋值
      for(int i=3;i<n;i++)
      {
          a[i]=(a[i-1]+a[i-2]+a[i-3])%10000;//算出每一个值就对其取余(前面的位数不考虑)
      }
      System.out.println(a[n-1]); //输出20190324项的结果
    }
    
}

动态规划：

public class qiujie{
	public static void main(String[] args) {
		int a = 1, b = 1, c = 1;
		// 要是求第四项，则i < 4, 同理推得求20190324，则i < 20190324。
		for (int i = 3; i < 20190324; i++) {
			int temp = (a + b + c) % 10000;
			a = b;
			b = c; //不断地更替三个数值，就可以减少重复计算中间值
			c = temp;
		}
		System.out.println(c);
	}
}

代码结果如下：
输出：4659

四、数的分解

问题描述
把 2019 分解成 3 个各不相同的正整数之和，并且要求每个正整数都不包含数字 2 和 4，一共有多少种不同的分解方法？
注意交换 3 个整数的顺序被视为同一种方法，例如1000+1001+18和1001+1000+18被视为同一种。
问题分析：
　　一开始就想着三个数字从0-2019循环暴力判断符合条件的输出，但是发现三层循环复杂度太大，最后选择两层循环，(第三个值=2019-第一个值-第二个值)。将判断不包含数字 2 和 4的情况写成一个Ok方法。
代码如下：

import java.util.Scanner;
public class Main{
	public static void main(String[] args) {
		Scanner input=new Scanner(System.in);
	      int n=input.nextInt();
	      int sum=0;
	      for(int i=1;i<=n/2;i++)//因为防止重复计数，因此i只能到n/2处
	      {
	    	  if(Ok(i))//如果满足条件去找j
	    	  {
	    		  for(int j=i+1;(j<n)&&(j<(n-i-j));j++)//各不相同所以j从i+1开始，并且满足第二个数小于第三个数(递增的思路)
	    		  {
	    			  int k=n-i-j;	 //直接用减法(减少三层循环的时间复杂度)
	    	    		if(Ok(j)&&Ok(k))
	    	    			 sum++;//满足条件就让结果可能+1
	    		  }
	    	  }
	      }
	      
	    	System.out.println(sum);  
	      
	}   

	private static boolean Ok(int i) {
  	  while(i!=0)
  	  {	  
  		  if(i%10==2||i%10==4)     //把数拆开如果有2和4有关就要返回错误(false)
  			  return false;
  		  else
  			  i=i/10;
  	  } 	  
		return true;
	}

}

代码结果如下：

五、特别数的和

问题描述
小明对数位中含有 2、0、1、9的数字很感兴趣（不包括前导 0），在1到40 中这样的数包括 1、2、9、10至32、39和40，共28个，他们的和是574。请问，在1到n中，所有这样的数的和是多少？
【输入格式】
输入一行包含两个整数 n。
【输出格式】
输出一行，包含一个整数，表示满足条件的数的和。
【样例输入】
40
【样例输出】
574
【评测用例规模与约定】
对于 20% 的评测用例，1 ≤ n ≤ 10。对于 50% 的评测用例，1 ≤ n ≤ 100。对于 80% 的评测用例，1 ≤ n ≤ 1000。对于所有评测用例，1 ≤ n ≤ 10000
问题分析：
　　这道题就是考虑将一个数字不断地拆开判断每一位是不是和四个数字有关系，然后编写一个判断函数duibudui()去判断，循环一个一个数字去判断。主要是判断的函数考虑%10取数(1234%10=4取出最后一位)，/10拆数(1234/10=123拆小一点)。
代码如下：

package xiaosai;
import java.util.Scanner;
public class Main{
	public static void main(String[] args) {
		Scanner input=new Scanner(System.in);
	      int n=input.nextInt();
	      int sum=0;
	      for(int i=1;i<=n;i++)//循环调用方法满足就sum加上当前值
	     {
	    	 if(duibudui(i))
	    		 sum+=i; 
	     }	      
	     System.out.println(sum);//输出最终值	     
	}
	
	public static boolean duibudui(int i)  //判断是不是满足题意
	{
		每次循环就是将数字拆小(直到最后拆没了就跳出来)
		while(i!=0)
		{
			if (i%10==2||i%10==0||i%10==1||i%10==9)//每次取出一位判断是不是和2/0/1/9四个数字有关(1234%10=4)
				return true;
			 i/=10;//将这个判断的数字拆小(1234/10=123)
		}
		return false;
	}
	
}

代码结果如下：

六、年号子串

问题描述
小明用字母 A 对应数字 1，B 对应 2，以此类推，用 Z 对应 26。对于 27 以上的数字，小明用两位或更长位的字符串来对应，例如 AA 对应 27，AB 对应 28，AZ 对应 52，LQ 对应 329。
请问 2019 对应的字符串是什么？
问题分析：
　　当时是手算的答案，现在下来仔细看了看也就是26进制，只不过就是拆一次数判断出来的结果放在数组之后要反序输出。
代码如下：

import java.util.Scanner;
public class Main{
	public static void main(String[] args) {
		Scanner input=new Scanner(System.in);
	      int n=input.nextInt();
	      char[] a={'A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'};//直接利用下标取数
	      char[] b=new char[10];
	      int m=1;
	      int i=0;
	      if(n<=26)
	    	  System.out.println(a[n-1]);//26之内就输出对应的结果
	      else
	      {
	    	  while(n!=0)
	    	  {
	    		  m=n%26;  //拆开这个数最低位判断输出哪个字母
	    		  b[i++]=a[m-1];//因为A是0，所以输出a[m-1]
	    		  n=n/26;  //然后将判断的数组拆成更小的数	    		
	    	  }  
	      }
	     	      
	      for(int j=b.length-1;j>=0;j--) //反序输出
	      {
	    	  if(b[j]!=0)
	    	  System.out.print(b[j]); 
	      }  
	      
	}	
}

代码结果如下：

七、等差数列

问题描述
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列，只记得其中N 个整数。
现在给出这N 个整数，小明想知道包含这N 个整数的最短的等差数列有几项？
【输入格式】
输入的第一行包含一个整数N。
第二行包含N 个整数
【输出格式】
输出一个整数表示答案。
【样例输入】
5
2 6 4 10 20
【样例输出】
10
【样例说明】
包含2、6、4、10、20 的最短的等差数列是2、4、6、8、10、12、14、16、18、20。
【评测用例规模与约定】
对于所有评测用例，2≤N≤1000002≤N≤100000
问题分析：
　　这道题其实主要是有坑(d=0的情况)，只需要将输入的数字存放在数组中然后排序之后找到两两之间最小的差就是d(因此输入的数字不一定是相邻的，可能是中间隔了好几个数)，利用等差数列的第An项公式：An=A1+(n-1)*d求出n就是所求的值
代码如下：

package xiaosai;
import java.util.Arrays;
import java.util.Scanner;
public class Main{
	public static void main(String[] args) {
		Scanner input=new Scanner(System.in);
	      int n=input.nextInt();
	      int[] a=new int[n];
	      for(int i=0;i<a.length;i++)
	      {
	    	  a[i]=input.nextInt();//输入数字
	      }
	      Arrays.sort(a);//排序
	      int d=100;
	      int cha=0;
	      for(int i=0;i<a.length-1;i++)
	      {
	    	 cha=a[i+1]-a[i];
	    	 if(cha<d)//依次两两判断最小的差距就是公式d
	    		 d=cha;
	      }
	      if(d==0)
	    	  System.out.println(n);
	      else
	      {
	    	  n=(a[a.length-1]-a[0])/d+1;//利用数组公式求出n(最小的就应该是排序之后的第一个和最后一个之间的数列)
	    	  System.out.println(n);
	      }	      
  }
}