蓝桥杯校赛

一、分核桃

  • 问题描述
    小张是软件项目经理，他带领3个开发组。工期紧，今天都在加班呢。为鼓舞士气，小张打算给每个组发一袋核桃（据传言能补脑）。他的要求是：
  1. 各组的核桃数量必须相同
  2. 各组内必须能平分核桃（当然是不能打碎的）
  3. 尽量提供满足1,2条件的最小数量（节约闹革命嘛）

输入格式
输入包含三个正整数a, b, c，表示每个组正在加班的人数，用空格分开（a,b,c<30）
输出格式
输出一个正整数，表示每袋核桃的数量。

样例输入1
2 4 5
样例输出1
20

样例输入2
3 1 1
样例输出2
3

  • 问题分析：
    　　很明显是两个两个人求最小公倍数的问题。
  • 1.暴力法：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
package xiaosai;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
	Scanner input=new Scanner(System.in);
	int a=input.nextInt();
	int b=input.nextInt();
	int c=input.nextInt();
	
	for(int i=1;i<1000;i++)
	{
		if(i%a==0&&i%b==0&&i%c==0)  //最小的值应该满足同时可以整除三个数字
		{
			System.out.println(i);
			break;
		}
	}
	
  }
}
  • 2.最小公倍数法：
  1. 求两个数的最大值。
  2. 从最大值开始循环找到第一个能够同时整除的数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
package xiaosai;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
	Scanner input=new Scanner(System.in);
	int a=input.nextInt();
	int b=input.nextInt();
	int c=input.nextInt();//输入三个数字
	int flag=0;//定义变量存储合适的那个值
	
	int d=zuida(a,b);//求前两数的最大值
	for(int i=d;;i++)//从前两数的最大值开始
	{
		if(i%a==0&&i%b==0) //只要能够整除
		{
			flag=i;//flag存储当前符合的最小公倍数
			break;
		}		
	}
	
	int e=zuida(flag,c); //求第二次的最大值
	for(int i=e;;i++) //从最大值开始
	{
		if(i%flag==0&&i%c==0)//只要能够整除
		{
			flag=i;//存储最终满足的值
			break;
		}		
	}
		
	System.out.println(flag); //输出答案
	
  }

	public static int zuida(int i,int j) {  //求两个数的最大值
		return i>j?i:j;
	}

}
  • 代码结果：

二、字符删除

  • 问题描述
    编写一个程序，先输入一个字符串str（长度不超过20），再输入单独的一个字符ch，然后程序会把字符串str当中出现的所有的ch字符都删掉，从而得到一个新的字符串str2，然后把这个字符串打印出来。　　

输入格式：输入有两行，第一行是一个字符串（内部没有空格），第二行是一个字符。　　
输出格式：经过处理以后的字符串。

样例输入
123-45-678-
样例输出
12345678

  • 问题分析：
    将字符串转为数组(toCharArray())，然后依次循环和ch字符对比，不相等就输出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
package xiaosai;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
	Scanner input=new Scanner(System.in);
	String str=input.nextLine();  //输入一个字符串
	char ch=input.next().charAt(0);  //输入一个字符
	char[] a=str.toCharArray(); //字符串转数组
	
	for(int i=0;i<a.length;i++)
	{
		if(a[i]!=ch)
			System.out.print(a[i]);  //不相等就输出
		
	}
	
  }
}
  • 代码结果：

三、区间K大数查询

  • 问题描述
    给定一个序列，每次询问序列中第l个数到第r个数中第K大的数是哪个。

输入格式
　　第一行包含一个数n，表示序列长度。
　　第二行包含n个正整数，表示给定的序列。
　　第三个包含一个正整数m，表示询问个数。

　　接下来m行，每行三个数l,r,K，表示询问序列从左往右第l个数到第r个数中，从大往小第K大的数是哪个。序列元素从1开始标号。

输出格式
　　总共输出m行，每行一个数，表示询问的答案。
样例输入
5
1 2 3 4 5
2
1 5 2
2 3 2
样例输出
4
2
数据规模与约定
　　对于30%的数据，n,m<=100；
　　对于100%的数据，n,m<=1000；

  • 问题分析：
    　　定义一个数组a先往里面放值，然后定义一个r-l+1长的数组b存放要截取的数组，然后定义一个ans数组存放每一次循环判断的最k大值(很关键)，然后输入l，r，k之后按顺序存放进数组b，一定要记得sort一下(不一定存放的数组就是顺序的！！！)，最后将最k大值放入ans数组！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import java.util.Arrays;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
		Scanner in = new Scanner(System.in);
		int n = in.nextInt();//输入数组的长度
		int[] a = new int[n];//定义一个n长度的数组a
		for(int i=0;i<n;i++)
		{
			a[i] = in.nextInt(); //一位一位输入内容
		}		
		int m = in.nextInt();//定义找几次
		int[] ans = new int[m];//按照m定义长度数组ans
	 for(int i=0;i<m;i++)//找几次就循环几次
		{
			int l = in.nextInt();//输入要选的左边值
			int r = in.nextInt();//输入要选的右边值
			int k = in.nextInt();//输入要选的第k大值
			int[] b = new int[r-l+1];//定义一个截取范围的数组b
			for(int j=0;j<r-l+1;j++)//从0到最大值赋值
			{
				b[j]=a[j+l-1];//依次将对应的值放入b数组中
			}
			Arrays.sort(b);//一定要记得排序(输入的数字不一定按顺序排列)
			ans[i]=b[r-l+1-k];//把那个最k大值放入ans数组值中
		}
		
        for(int i=0;i<m;i++)
		{
			System.out.println(ans[i]);//依次输出的就是找几次的对应的答案
		}

	}

}
  • 代码结果：

四、阶乘(第一个非0数)

  • 问题描述
    　　一个整数n的阶乘可以写成n!，它表示从1到n这n个整数的乘积。阶乘的增长速度非常快，例如，13!就已经比较大了，已经无法存放在一个整型变量中；而35!就更大了，它已经无法存放在一个浮点型变量中。因此，当n比较大时，去计算n!是非常困难的。幸运的是，在本题中，我们的任务不是去计算n!，而是去计算n!最右边的那个非0的数字是多少。例如，5! = 12345 = 120，因此5!最右边的那个非0的数字是2。再如：7! = 5040，因此7!最右边的那个非0的数字是4。请编写一个程序，输入一个整数n(n<=100)，然后输出n!
    最右边的那个非0的数字是多少。
    　　
    　　输入格式：输入只有一个整数n。
    　　输出格式：输出只有一个整数，即n! 最右边的那个非0的数字。输入输出样例

样例输入
6
样例输出
2

由于只需要阶乘后的最后一个非０数，所以每次阶乘后，如果尾数是０的直接／１０。

  • 问题分析：
  1. 先编写一个递归方法求每一个数对应的阶乘。
  2. 将结果暂存在数组内，然后设置变量m来遍历直至第一个非0数就跳出判断。

解法一(30%)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
package xiaosai;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
	Scanner input=new Scanner(System.in);
	int n=input.nextInt();
	int[] a=new int[1000];
	a[0]=jiecheng(n);
	int m=1;
	for(int i=0;;i++)
	{
		m=a[0]%10;
		if(m!=0)
		{
			System.out.println(m);	
			break;
		}
		a[0]=a[0]/10;		
	}		
}
	
	public static int jiecheng(int n) {
		if(n==0||n==1)
			return 1;
		else 
			return n*jiecheng(n-1);		
	}  
}
  • 问题分析：
  1. 和解法一相似使用数组一个数字存放数组一个元素之中得到结果。
  2. 循环每次判断结果和考虑进位问题以此类推得到结果，最终还是循环判断非0数。

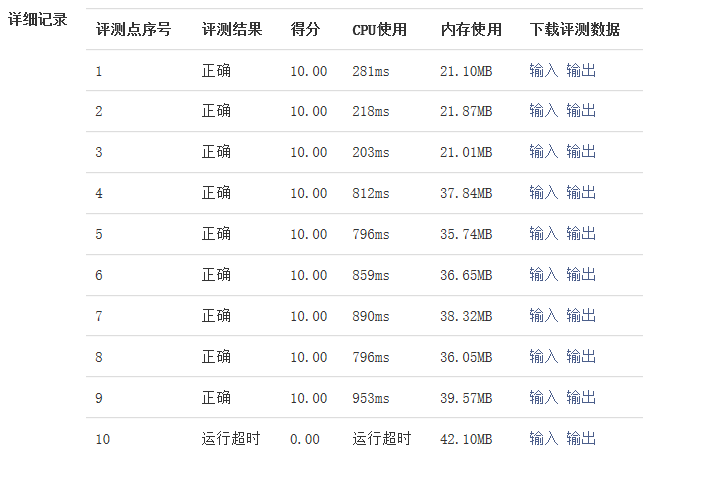
解法二(100%)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
package xiaosai;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		int a[]= new int[4000];
		a[0]=1;
		int r1=0;//考虑进位情况
		for(int i=2;i<=n;i++) {
			for(int j=0;j<4000;j++) {
				r1=a[j]*i+r1;
				a[j]=r1%10;  //如果发生进位将个位赋给当前位置，十位或者和百位一起加到下一次数组乘法
				r1=r1/10;   //依次类推
			}
		}
		int s=0;
		for(int i=3999;i>=0;i--) {
			if(a[i]!=0) {
				System.out.print(a[i]);  //从后往前倒排，然后判断首位不为空则输出
				s=i;   //同时记录下标
				break;
			}
		}

	}
}
  • 问题分析：
  1. 像解法一一样，如果用int型和递归方法会导致超时等问题，所以考虑使用BigDecimal类型存放结果。
  2. 考虑将结果用tosrtring方法转化为字符串，通过

charAt方法来循环判断是否为0找到最终结果。

解法三(100%)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
package xiaosai;
import java.util.Scanner;
import java.math.*;
public class Main {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int n = input.nextInt();
		BigDecimal sum = BigDecimal.ONE;//使用BigDecimal类型存放答案
		for(int i = 1; i <= n; i++) 
		{
			sum = sum.multiply(BigDecimal.valueOf(i));//使用乘法(不使用递归方法！)
		}

	String S = sum.toString(); //将结果转化为字符串
		for(int i = S.length()-1; i >= 0; i--)
		{
			if(S.charAt(i) != '0')//遇到第一个非0的数字输出 
			{
				System.out.println(S.charAt(i));
  			      break;
			}
		}
	
	}
}

代码结果如下:

五、最长子序列

  • 问题描述
    给定一个长为n的序列，求它的最长上升子序列的长度。
    输入格式
    　　输入第一行包含一个整数n。
    　　第二行包含n个整数，为给定的序列。
    输出格式
    　　输出一个非负整数，表示最长上升子序列的长度。
    样例输入
    5
    1 3 2 5 4
    样例输出
    3
    数据规模和约定
    　　0<n<=1000，每个数不超过10^6。

  • 问题分析：
    例如：数列(1, 7, 3, 5, 9, 4, 8)的有序上升子序列，像(1, 7)， (3, 4, 8)和许多其他的子序列。在所有的子序列中，最长的上升子序列的长度是4，如(1, 3, 5, 8)

  • 动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
package xiaosai;
import java.math.*;
import java.util.Scanner;
public class Main{
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in); 
		int n = input.nextInt();
		int[] arr = new int[10002];//arr数组表示输入的序列
		int[] dp = new int[10002];//dp数组中存放上升序列的长度，dp[i]表示以arr[i]结尾的子序列的最大长度
		for(int i = 1;i <= n;i++) {//输入序列
			arr[i]= input.nextInt();
		}
		
		int result = -1;//记录dp中最大的值				
		for(int i = 1;i <= n;i++)
		{//按顺序计算dp[i]的值			
			dp[i] = 1;//假设该子序列中只有arr[i]，故长度为1，即其自身成为一个子序列			
			for(int j = 1;j < i;j++) 
			{//如果在i之前有比arr[i]小的数(arr[j])，并且把该数(arr[i])放到以arr[j]结尾的子序列末尾后，//其长度比当前以arr[i]结尾的子序列长度要长				
				if(arr[i] > arr[j] && dp[j] + 1 > dp[i]) 
				{					
					dp[i] = dp[j] + 1;//把arr[i]放到以arr[j]结尾的子序列之后，原来的长度＋1				
				}			
			}
			result = Math.max(result, dp[i]);//找出在dp数组中最大的一个，即子序列长度最长的一个		
		}
		 System.out.println(result);	
		 }
	}

代码结果如下：

赏

×

纯属好玩

扫码支持
扫码打赏，你说多少就多少

打开支付宝扫一扫，即可进行扫码打赏哦

本文标题:蓝桥杯校赛

文章作者:Larkkkkkkk

发布时间:2019年11月07日 - 15时41分

最后更新:2020年03月15日 - 15时34分

原始链接:https://larkkkkkkk.github.io/2019/11/07/%E8%93%9D%E6%A1%A5%E6%9D%AF%E6%A0%A1%E8%B5%9B/

许可协议: "署名-非商用-相同方式共享 3.0" 转载请保留原文链接及作者。

文章目录
,