2019-10-15

贪心算法

贪心算法：
　　又称贪婪算法。重复地使用一个贪婪规则（确定一个符合的准则）去挑选解的一部分，从局部最优解逐步达到全局最优。
　　贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。
例如：
背包问题：
有三个参赛者：A,B,C;
每个比赛者一个包（包的载重量为20kg）
给定N个物品，每个物品有一定的质量和价值
规则：
　　１.物品可以切一部分放入
　　2.包装的物品的总质量不超过包的载重量
　　3.包里装的物品的价值之和最高者获胜
假设：物品n=3，包的载重量c=20
物品1:V=25,M=18
物品2:V=24,M=15
物品3:V=15,M=10

思路：
A考虑优先放入价值高的物品：
　　max=25+24（2/15）=28.2;
B考虑优先放入重量低的物品：
　　max=15+24（10/15）=31;
C考虑优先放入性价比高的物品：
　　max=24+15（5/10）=31.5;
*所以说我们对于此题选择C考虑的方法为解决题目的贪心规则。**

一、两地调度：
公司计划面试 2N 人。第 i 人飞往 A 市的费用为 costs[i][0]，飞往 B 市的费用为 costs[i][1]。
返回将每个人都飞到某座城市的最低费用，要求每个城市都有 N 人抵达。
示例：
　　输入：[[10,20],[30,200],[400,50],[30,20]]
输出：110
解释：
　　第一个人去 A 市，费用为 10。
　　第二个人去 A 市，费用为 30。
　　第三个人去 B 市，费用为 50。
　　第四个人去 B 市，费用为 20。

思路：
　　我们可以考虑先让公司指派2N个人全都去A城，然后计算从A和B出发的金钱差额放入数组里面，排序之后将数组前一半的人替换到B去，这样可以保证有N个人去A，其他人去B。然后也可以保证最低费用。

import java.util.Scanner;
import java.util.Arrays;
public class DiYiGe{
	public static void main(String[] args) {
	   Scanner input=new Scanner(System.in);
	   int n=input.nextInt();
	   int m=input.nextInt();
	   int[][] a=new int[n][m];
	   for(int i=0;i<n;i++)
	   {
		   for(int j=0;j<m;j++)
		   {
		     a[i][j]=input.nextInt();  //双层循环读取分别去A和B的花费
		   }
	   }
	    System.out.println(min(a));	   
	}	
	
	    public static int min(int[][] a) {
	        int m=a.length;  //原数组的长度
	        int b[] = new int[m];  //对应存放每个人去A和B的消耗差
	        int sum = 0;  
	        for(int i=0;i<m;i++){
	            b[i] = a[i][1]-a[i][0];  //计算从A到B城的消耗差
	            sum +=a[i][0];   //加上所有人到A城的费用
	        }
	        Arrays.sort(b); //将差距
	        for(int i=0;i<m/2;i++)
	            sum+=b[i];    //减去应到B城的人员的额外消耗
	        return sum;
	    }
}

代码结果如下：

二、柠檬水找零：
　　在柠檬水摊上，每一杯柠檬水的售价为 5 美元。
　　顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。
每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。
　　注意，一开始你手头没有任何零钱。

示例：
　　输入：[5,5,5,10,20]
　　输出：true
解释：
　　前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
　　第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
　　第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
　　由于所有客户都得到了正确的找零，所以我们输出 true。

思路：先收前面的人钱，然后保证手里有零钱，如果需要找20的话，先考虑找10元大的钱，保证5元够用。

import java.util.Scanner;
public class NingMeng {
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        int n=input.nextInt();
        int[] a=new int[n];
        for(int i=0;i<n;i++)
        {
            a[i]=input.nextInt();
        }
        System.out.println(Change(a));
    }

    public static boolean Change(int[] a) {
        int money[] = new int[3];  // 利用下标存放5/10/20元的数量
        money[0]++;  //存放5元的个数
        for (int i=1;i<a.length;i++) {
            switch (a[i]) {  //依次找零
                case 5:
                    money[0]++;  //如果是5元直接+1
                    break;
                case 10:
                    money[1]++;  //十元的话+1
                    money[0]--;  //找零5元
                    if (money[0] < 0) {
                        return false;  //不能成功找零
                    }
                    break;
                case 20:
                    money[2]++; //如果是20元直接+1
                    if (money[1]>0) { //如果有10元找一张 10元-1 5元-1
                        money[1]--;
						money[0]--; 
                    }
                    else {
                        money[0] -= 3;  //如果找5元 5元-3
                    }

                    if (money[0] < 0) {
                        return false;
                    }
                    break;
            }
        }
        return true;
    }
}

代码结果如下：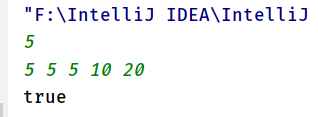

三、跳台阶
给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
例如：
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。
说明：假设你总是可以到达数组的最后一个位置。
思路：
假如a={2,3,1,1,4,2,1}那么最符合题意的就是2跳到3的位置然后跳到4然后跳到终点。
现在当处于第一个位置2的时候考虑是跳到3还是1，显然跳到3更好一点，那么跳到3之后考虑跳到1还是1还是4，因此选择4的位置，最后选择跳到终点。
->我们考虑下一个要跳跃的点就必须是保证上一次和这一次的跳跃点距离最远，这样可以保证输出少。

贪心算法代码：

  public int jump(int[] a) {
     int sum = 0;
      int zy = 0; // 能跳到的最远距离
      int max = 0; // 下一步可以跳到的最远距离
      for(int i = 0; i < a.length - 1; i++)
{
          max = Math.max(max, i + a[i]);
          // 更新当前点
          if(i == zy)
	{
              zy = max;
              sum++;
          }
      }
      return sum;
  }